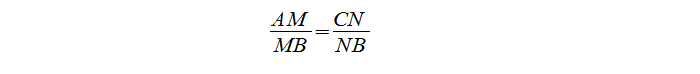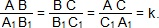Что значит подобны в геометрии

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Определение и знак подобия в геометрии

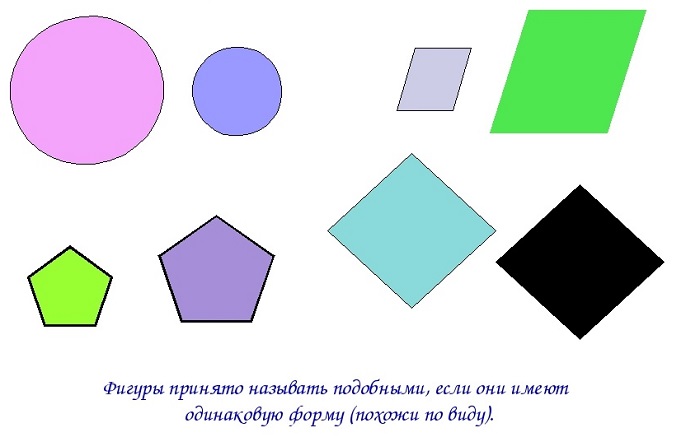
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A₁B₁C₁ считаются подобными при равнозначности углов и пропорциональности сторон;

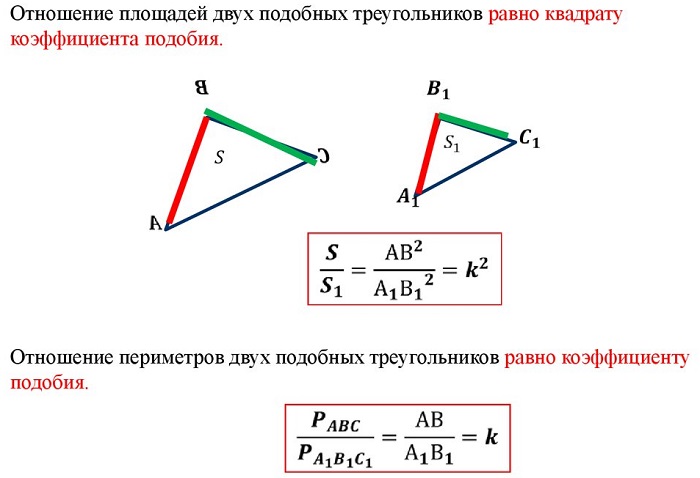
отношение площадей подобных треугольников равно квадрату коэффициента подобия.

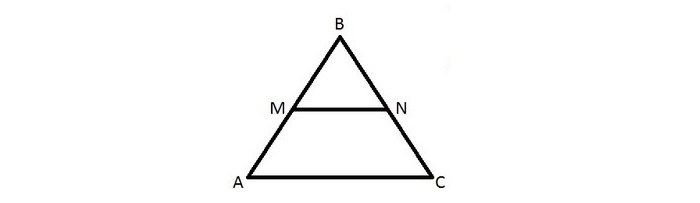
Доказательство подобия треугольников через среднюю линию

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

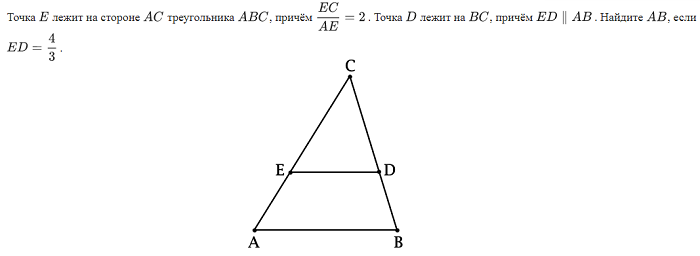
Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник

Знак подобия в геометрии — правило и примеры обозначения

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Определение и знак подобия в геометрии

Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.

На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;

отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство подобия треугольников через среднюю линию

Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник

Подобие фигур

Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.

Содержание:

Понятие подобия фигур

В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.

Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.

Для обозначения подобия фигур употребляется знак . На рисунке 2.434 изображены подобные фигуры . Запись читается: фигура подобна фигуре

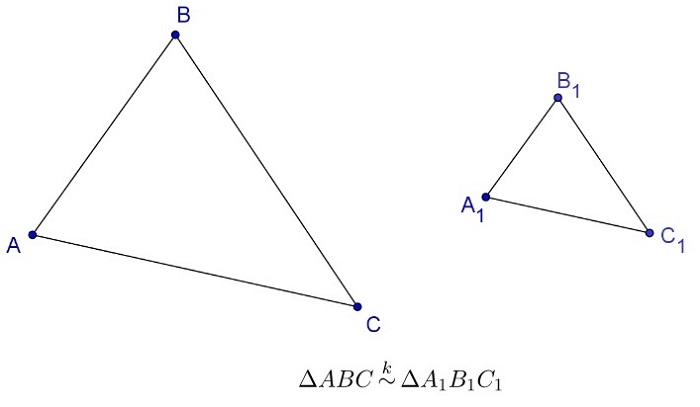
Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.

Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.

Определение. Масштаб — это коэффициент подобия соответствующих фигур.

Подобие треугольников

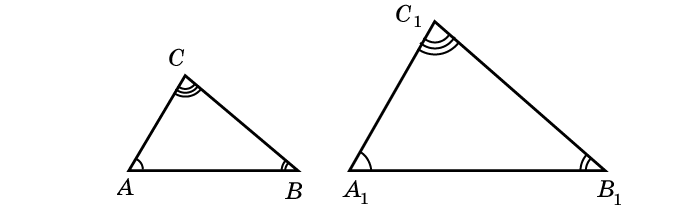
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны: Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.

Подобие треугольников записывается так: Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников будет число 2. Если же взять отношения , коэффициент подобия будет равен .

Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.

Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.

Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.

Для выявления подобия треугольников существуют признаки подобия треугольников.

Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Следствия из этой теоремы.

1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.

Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Подобие многоугольников

Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.

Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).

Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).

Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Глоссарий. Алгебра и геометрия

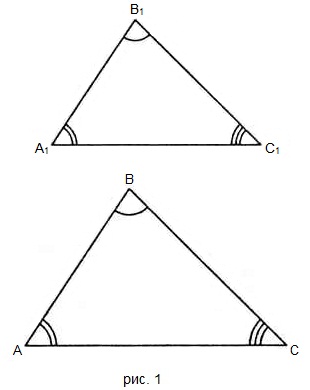
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A₁B₁C₁ так, что

A = A₁, B = B₁, С = С₁,

Число k, равное отношению сходственных сторон треугольника называется коэффициентом подобия.
Подобие треугольников ABC и A₁B₁C₁ обозначается так:

∆ A₁B₁C₁. На рисунке 1 изображены подобные треугольники.

Источник

Что такое треугольник: определение, классификация, свойства

Определение прямой

Определение прямой начинается с определения линии. Что такое линия? Это множество точек, соединенных между собой. Линия может быть прямой, кривой, ломанной, непрерывной и даже разомкнутой. И именно из-за этого разнообразия линии очень трудно определить в пространстве. Непонятно, как пройдет та или иная кривая, когда выйдет за пределы листа. Поэтому был выделен отдельный вид линий – прямые.

Когда в разговоре вы слышите прямая – люди имеют в виду прямую линию, но последнее слово в словосочетании принято опускать.

Что такое прямая в математике? Прямые это бесконечные непрерывные линии, которые не имеют искривлений. Первое правило линий: через любые две точки можно провести линию. А вот через три точки уже не всегда. Чаще всего через три точки можно провести три прямых.

Если прямая проходит через три точки, то про эти точки говорят, что они лежат на одной прямой. Прямые, как правило, обозначают малой латинской буквой или по названию двух точек на прямой.

Почему двух, а не трех? Очень просто: через две точки может пройти только одна прямая. Тогда как через одну: бесконечное множество. А три точки не имеет смысла использовать: ни к чему усложнять обозначение.

Определение и обозначение подобных треугольников

Подобными называются треугольники, у которых углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.

Сходственные стороны в подобных треугольниках – это стороны, лежащие напротив их равных углов.

Для обозначения подобия фигур используется специальный символ “∼“. Например, △ABC ∼ △KLM.

Определение треугольника

Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.

Углы можно, также, обозначать с помощью специального знака “∠“:

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.

2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Прямая линия. Уравнение прямой.

Основная информация по курсу геометрии для обучения и подготовки в экзаменам, ГВЭ, ЕГЭ, ОГЭ, ГИАПрямая линия. Уравнение прямой.

Свойства прямой

1. Через любые две точки можно провести только одну прямую линию.

Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.

2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.

3. Через одну точку можно провести бесконечно много прямых.

4. Есть точки лежащие на прямой и не лежащие на ней.

Точки N и M лежат на прямой a. Точка L не лежит на прямой a.

Для записи принадлежности точки к прямой используется символ принадлежности – ∈. Например, запись M ∈ a обозначает, что точка M принадлежит прямой a. Для того, чтобы указать что точка не принадлежит прямой можно использовать символ ∉. Например, запись L ∉ a обозначает, что точка L не принадлежит прямой a.

5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.

6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.

Основные признаки делимости.

Признак делимости – правила с помощью которого можно относительно бегло найти, является ли число кратным предварительно выбранному.Основные признаки делимости.

Типы треугольников

По величине углов

сумма углов треугольника равна 180°.

Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

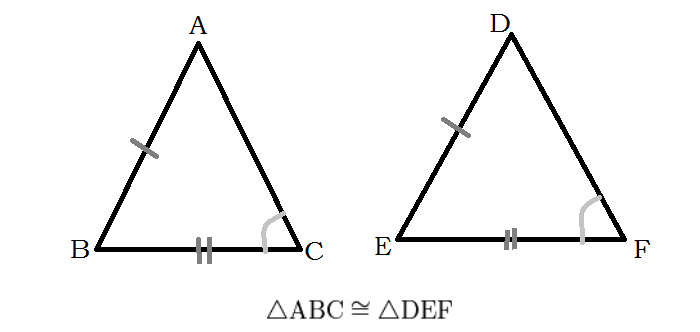
Признаки равенства треугольников

Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности ) можно определить по следующим тройкам основных элементов:

Признаки равенства прямоугольных треугольников:

В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.

Окружность описанная вокруг треугольника

Вычисление площади треугольника в пространстве с помощью векторов

Источник