Что значит периодическая функция

Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

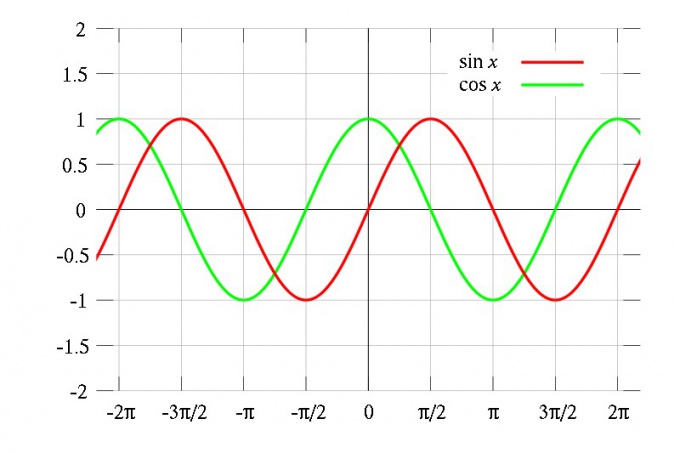
1) Поскольку для любого x выполняются равенства

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство =, то функция дробной части числа y= — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=.

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

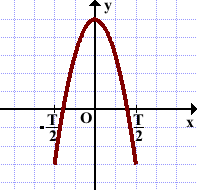
График периодической функции повторяется через промежутки длиной T (на оси Ox).

Дана часть графика

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Источник

Как определить периодичность функции

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Источник

Периодические функции

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Например, — периодические функции.

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Источник

Уроки математики и физики для школьников и родителей

суббота, 4 сентября 2021 г.

Урок 5. Периодичность тригонометрических функций

Из этого определения сразу следует, что если Т – период функции

– также периоды функций. Значит у периодической функции бесконечно много периодов.

Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :

Следовательно, при любом значении х

sin (α + 360 ° ) = sin α

Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.

где k – любое целое число.

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.

отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:

где k – любое целое число.

вычисляются по формуле

равен наименьшему числу, при делении которого на T ₁ и T ₂ получаются целые числа.

Найти период функции

не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.

Периода не существует.

Доказать следующее утверждение :

Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :

Доказать следующее утверждение :

Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

Доказать следующее утверждение :

Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :

Найти основной период функции

Пусть Т основной период функции, тогда:

так как 2 πk период синуса, то получим :

sin (7х + 7 t ) = sin (7х + 2 πk ),

Найти основной период функции

Пусть Т основной период функции, тогда:

со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )

так как 2 πk период косинуса, то получим :

Найти период функции :

y = 5 sin 2 x + 2 ctg 3х.

Наименьшее число, при делении которого на

Найти период функции :

Находим периоды слагаемых. Период функции

Очевидно, что период заданной функции равен

Найти период функции :

Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

Найти период функции :

Приведём к общему знаменателю периоды :

Тогда наименьшее общее кратное (НОК) будет :

Теперь найдём период заданной функции :

Источник

«Переодические функции»

Муниципальное образовательное учреждение

Лицей №5 имени Ю.А.Гагарина

Сведения об авторе:

Безрукова Ольга Леонидовна

высшая квалификационная категория,

педагогический стаж 35 лет

Тема урока : Периодические функции

Тип урока : Урок обобщения и систематизации знаний.

Цели и задачи урока :

1. Образовательные: формирование у обучающихся представлений о периодичности функции

2. Развивающие : развитие логического мышления, математически грамотной речи, умения четко и кратко излагать свои мысли

3. Воспитательные : воспитание добросовестного отношения к учебе, трудолюбия, аккуратности

a. добиваться понимания употребляемых терминов, алгоритма нахождения наименьшего положительного периода функции

b. построение графика периодичной функции

c. расширить кругозор учащихся по данной теме

d. развивать навыки сравнения, аналогии, обобщения изучаемого материала

5. Оборудование урока

a. Мультимедийный проектор

1. Организационный момент (1-2 минуты)

Учитель здоровается с детьми. Сегодня мы с вами обобщим и систематизируем свойства очень жизненно-важных функций. Каких именно, вы можете определить, посмотрев видеоролик. Очень кстати нам слова В.Гёте: «Просто знать – еще не все, знания нужно уметь использовать»

Дети приветствуют учителя, садятся. Смотрят видеоролик о смене времен года, выбросе воды из гейзера, сокращении сердечной мышцы, о морских приливах и отливах и т.д.

2. Актуализация знаний

Как вы думаете, какие функции характеризуют природные явления, которые вы сейчас увидели на экране?

Дети формулируют название функций, характеризующих явления, тем самым формулируется тема урока.

3. Фронтальный опрос

1) Какая функция называется периодической?

2) Что является периодом постоянной функции?

3) Какой период называется основным?

4) Какие основные периодические функции вам известны?

5) Как найти период функций y = sin ( kx + b )

Назовите период функции: ; ;

6) Как найти период суммы тригонометрических функций?

7) Всегда ли возможно непосредственное нахождение периода функций? Например,

8) Каким свойством обладают графики периодических функций?

9) Является ли число 8 π периодом функции ?

10) При каких значениях параметра а функция f ( x )= ax +2 является периодической? При каких значениях параметра а функция является периодической?

11) Где в жизни, на практике мы встречаемся с периодическими процессами и явлениями?

Дают соответствующие определения

4. Применение знаний и умений

Учащимся предлагаются карточки с заданиями к уроку:

1. Найти период функции

2. Докажите, что число 2 π является периодом функции:

3. Нечетная функция определена на всей числовой прямой и является периодической с периодом 7. Найдите значение выражения:

, если f(-3)=2

4. Функция f ( x ) определена на всей числовой прямой и является периодической с периодом 8. На рисунке изображен график этой функции при . Найдите значение выражения f (5)+ f (10)+ f (15). Два способа решения, возможен нерациональный графический метод решения.

1. Простейшие упражнения для глаз.

2. Обязательные упражнения для улучшения мозгового кровообращения: медленно наклонить голову вперед и назад 3-4 раза.

f ( x ) – периодическая функция с периодом T = . Найти значение , если известно, что

и

7. Подведение итогов урока

Итак, мы сегодня повторили и обобщили понятие периодической функции и ее свойства, их использования при решении задач. Еще раз, какие типы задач связаны с применением свойств периодических функций:

Периодическая функция и ее свойства

2) Доказать, что Т – период

3) Построить график периодической функции

4) Использование свойств периодичности при решении задач

8. Домашнее задание

1) Творческое задание (по желанию) – реферативно приготовить сообщение по теме. Это может быть народное творчество, орнамент, явления природы, живого организма, вред колебательных движений (Например, почему военные никогда не маршируют по мосту) и т.д.

2) Доказать, что Т= π является периодом функции

3) Найти период функции

.

Найдите значение выражения 2* f (-12) – 3* f (21)

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Краткое описание документа:

Урок обобщения и систематизации знаний по теме «Переодические фукции» с хорошей подборкой нестандартных задач, позволяющих закрепить свойства переодических фукций, показать их существование в природе, что несомненно доказывает важность изучения темы и ее практическое приложение. За счет небольшого видеоролика о смене времен года, выбросе воды из гейзера, полета птиц, сокращения сердечной мышцы и т.д. дети могут сами сформулировать определение фукции, характерезующих эти явления, а тем самым формулируется и тема урока.

Общая информация

Похожие материалы

Урок обучения грамоте «Моё Отечество»

Урок- консультация по математике для 11 класса « Решение задач на сплавы, смеси»

Разработка урока по геометрии по теме: «Площадь треугольника»

Внеклассное мероприятие по математике «Математика вокруг нас»

Урок математики 6 класс «Координатная плоскость.Прямоугольная система координат»

Развитие критического мышления на уроках математики

Интегрированный урок по математике и природоведению

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5360620 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

В России предложили учредить День семейного волонтерства

Время чтения: 2 минуты

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Создана Ассоциация руководителей школ России и Беларуси

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник