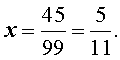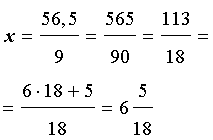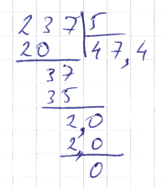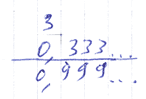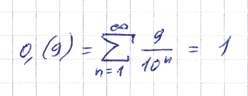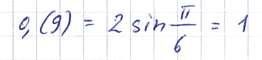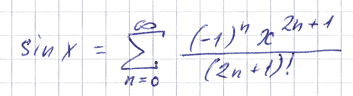Что значит периодическая дробь
Периодическая дробь
Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.
| обыкновенная дробь | десятичная дробь |
|---|---|
| 4 /10 | 0,4 |
| 79 395 /1000 | 79,395 |
Очевидно, в начало целой части и/или в конец дробной части можно дописывать сколько угодно нулей.
Существуют также бесконечные десятичные дроби — периодические и непериодические. Например, ⅓ записывается как бесконечная периодическая дробь 0,3333… или 0,(3). А число π записывается как бесконечная непериодическая дробь 3,141592…
Периодическая десятичная дробь называется чистой периодической дробью, если её период (группа повторяющихся цифр) начинается сразу после запятой, а период может содержать любое конечное число цифр. Так, дробь 1,(3) — чистая периодическая дробь. Если периодическая десятичная дробь содержит ещё число, заключённое между целой частью и периодом, то такая периодическая дробь называется смешанной; число периодической дроби, стоящее между целой частью и периодом, называется предпериодом этой дроби.
Очевидно, что всякая периодическая дробь является рациональным числом вида 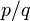
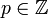
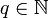
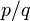
Произношение десятичных дробей
В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» («целая»), потом десятичная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.).
Однако на практике часто встречается такое произношение: целая часть, союз «и», дробная часть.
Бесконечные периодические и непериодические десятичные дроби
Содержание
Бесконечные периодические и непериодические десятичные дроби
В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.
В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.
Бесконечные десятичные дроби бывают периодическими и непериодическими.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь
Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.
ОТВЕТ : 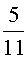
ОТВЕТ : 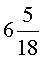
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Бесконечные периодические дроби
К сожалению, некоторые люди считают, что если они знают теорию рядов, то значит без неё никаких метаматических понятий вводить нельзя. Более того, эти люди полагают, что тот, кто не использует её повсеместно, — невежда. Оставим воззрения этих людей на их совести. Давайте лучше разберёмся с тем, что такое бесконечная периодическая дробь и как с ней быть нам, необразованным людям, не знающим пределов.
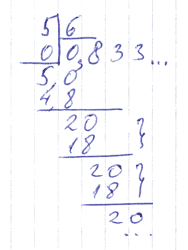
Поделим 237 на 5. Нет, не нужно запускать «Калькулятор». Давайте лучше вспомним среднюю (или даже начальную?) школу и просто поделим столбиком:
Ну как, вспомнили? Тогда можно и к делу переходить.
Понятие «дробь» в математике имеет два значения:
Существует два вида дробей — в смысле, две формы записи нецелых чисел:
Заметим, что вообще само использование дроби-записи не означает, что записанное есть дробь-число, например 3/3 или 7,0 — не дроби в первом смысле слова, но во втором, конечно, дроби.
В математике, вообще искони принят счёт десятичный, а потому и десятичные дроби удобнее простых, т. е. дробь с десятичным знаменателем (Владимир Даль. Толковый словарь живого великорусского языка. «Десять»).
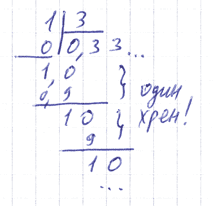
А раз так, то хочется всякую дробь вертикальную сделать десятичной («горизонтальной»). А для этого нужно просто-напросто числитель поделить на знаменатель. Возьмём, например, дробь 1/3 и попробуем сделать из неё десятичную.
Даже совсем необразованный заметит: сколько ни дели — не разделится: так и будут тройки до бесконечности появляться. Так и запишем: 0,33. Имеем в виду при этом «число, которое получается, когда делишь 1 на 3», или, короче, «одна третья». Естественно, что одна третья — дробь в первом смысле слова, а «1/3» и «0,33. » — дроби во втором смысле слова, то есть формы записи числа, которое находится на числовой прямой на таком расстоянии от нуля, что если трижды его отложить, получится единица.
Теперь попробуем разделить 5 на 6:
Снова запишем: 0,833. Имеем в виду «число, которое получается, когда делишь 5 на 6», или, короче, «пять шестых». Однако, тут возникает путаница: имеется ли в виду 0,83333 (и дальше тройки повторяются), или же 0,833833 (и дальше 833 повторяется). Поэтому запись с многоточием нас не устраивает: непонятно, откуда начинается повтряющаяся часть (она называется «период»). Поэтому период мы будем брать в скобки, вот так: 0,(3); 0,8(3).
0,(3) не просто равно одной третьей, это есть одна третья, ведь мы специально эту запись придумали, чтобы представлять это число в виде десятичной дроби.
Эта запись и называется бесконечной периодической дробью, или просто периодической дробью.
Всегда, когда мы делим одно число на другое, если не получается дробь конечная, то получается дробь бесконечная периодическая, то есть обязательно когда-нибудь последовательности цифр начнут повторяться. Почему это так можно понять чисто умозрительно, посмотрев внимательно на алгоритм деления столбиком:
В местах, обозначенных галочками, не могут всё время получаться разные пары чисел (потому, что таких пар в принципе конечное множество). А как только там появится такая пара, которая уже была, разность тоже будет такой же — и дальше весь процесс начнёт повторяться. Нет нужды проверять это, ведь совершенно очевидно, что при повторении тех же действий результаты будут те же.
Теперь, когда мы хорошо понимаем суть периодической дроби, давайте попробуем умножить одну треть на три. Да, получится, конечно, один, но давайте запишем эту дробь в десятичной форме и умножим столбиком (двусмыслицы из-за многоточия здесь не возникает, так как все цифры после запятой одинаковые):
И снова мы замечаем, что всё время будут после запятой появляться девятки, девятки и девятки. То есть, используя, обратно, скобочную запись, мы получим 0,(9). Поскольку мы знаем, что произведение одной трети и трёх есть единица, то 0,(9) — это такая вот причудливая форма записи единицы. Однако использовать такую форму записи нецелесообразно, ведь единица прекрасно записывается и без использования периода, вот так: 1.
Как видим, 0,(9) — это один из тех случаев, когда целое число записано в форме дроби, вроде 3/3 или 7,0. То есть, 0,(9) — это дробь лишь во втором смысле слова, но никак не в первом.
Вот так, безо всяких пределов и рядов мы разобрались с тем, что такое 0,(9) и как с ним бороться.
Но всё же вспомним о том, что на самом-то деле мы умные и изучали анализ. Действительно, трудно отрицать, что:
Но, пожалуй, никто не будет спорить и с тем, что:
Всё это, конечно, верно. Действительно, 0,(9) является и суммой приведённого ряда, и удвоенным синусом указанного угла, и натуральным логарифмом числа Эйлера.
Но ни то, ни другое, ни третье не является определением.
Утверждать, что 0,(9) — сумма бесконечного ряда 9/(10 n ), при n от единицы, — это всё равно, что утверждать, что синус — это сумма бесконечного ряда Тейлора:
Это совершенно верно, и это является важнейшим фактом для вычислительной математики, но это не определение, и, что самое главное, это ничуть не приближает человека к пониманию сути синуса. Суть же синуса некоторого угла состоит в том, что это всего навсего отношение противолежащего углу катета к гипотенузе.
Дак вот, периодическая дробь — это всего навсего десятичная дробь, которая получается, когда при делении столбиком один и тот же набор цифр повторется. Анализа тут нет и в помине.
И вот тут-то возникает вопрос: откуда вообще мы взяли число 0,(9)? Что на что мы делим столбиком, чтобы его получить? Действительно, нет таких чисел, при делении которых друг на друга столбиком мы бы имели бесконечно появляющиеся девятки. Но нам же удалось получить это число, умножая столбиком 0,(3) на 3? Не совсем. Ведь умножать нужно справа налево, чтобы корректно учитывать переносы разрядов, а мы это делали слева направо, хитро воспользовавшись тем, что переносов нигде всё равно не возникает. Поэтому правомерность записи 0,(9) зависит от того, признаём ли мы правомерность такого умножения столбиком или нет.
Осталось лишь добавить, что если бы мы использовали, скажем, троичную систему счисления, то при делении столбиком единицы (13) на тройку (103) получилось бы 0,13 (читается «ноль целых одна третья»), а при делении единицы на двойку получилось бы 0,(1)3.
Так что периодичность дроби-записи — это не объективная какая-то характеристика дроби-числа, а всего лишь побочный эффект использования той или иной системы счисления.
Перевод периодической дроби в обыкновенную дробь
Содержание
Периодические дроби – очень интересное явление. Только представьте себе дробь, у которой нет конца, и её «хвост» длится и длится.
Иногда возникает необходимость записать периодическую дробь в виде обыкновенной. Получается, что вместо числа мы пишем пример – ведь знак дроби обозначает знак деления.
Давайте разберёмся, как это сделать.
Состав периодической дроби
Прежде чем мы начнём превращать периодические дроби в обыкновенные, нам необходимо разобраться, как называются части периодических дробей. Это нам понадобится.
Итак, на первом месте – целая часть периодической дроби.
Всё, что после запятой, будет дробной частью.
У чистых периодических дробей дробная часть состоит из периода (повтораяющейся части дроби). Она взята в скобки. В скобках может быть не одна, а несколько цифр. Количество цифр в скобках называется длиной периода.
В смешанной периодической дроби между запятой и периодом есть ещё одна или несколько цифр. Эти цифры в период не входят, то есть не повторяются. Надо сказать, что в разных пособиях эта часть дроби может называться по-разному. Иногда ей не дают никакого названия, и просто пишут «цифры между запятой и периодом». Но также эту часть называют непериодической частью или предпериодом.
Перевод чистых периодических дробей в обыкновенные дроби
С чистыми периодическими дробями (то есть с теми, у которых период начинается сразу после запятой) всё очень просто. Для них существует простой алгоритм.
После того, как дробь записана, её можно сократить, разделив числитель и знаменатель на одинаковое число.
Перевод смешанных периодических дробей в обыкновенные дроби
Со смешанными дробями дело обстоит сложнее, тут нужно запомнить более длинный алгоритм действий. Кроме того, нужно хорошо знать названия всех частей периодической дроби, чтобы не запутаться.
Для перевода смешанной периодической дроби в обыкновенную нужно:
1) записать целую часть дроби (если она есть) без изменений
2) записать в виде числителя разность дробной части периодической дроби (записываем её без скобок, как если бы это было натуральное число) и предпериода (непериодической части) дроби
3) записать в виде знаменателя число, состоящее из девяток и нулей, где число девяток равно длине периода, а нулей – длине предпериода.
Выглядит очень длинно и сложно! Но проделав подобные вычисления несколько раз, вы сможете выполнять их без особого труда.
Целую часть записываем без изменений, переходим к дробной.
Разберём ещё один пример.
В знаменателе пишем одну девятку, так как длина периода равна одному, и два ноля, так как в непериодической части дроби у нас две цифры.
Уже после того, как вы переведёте несколько периодических дробей в обыкновенные, вы почувствуете, что алгоритм запомнился и уже не кажется таким сложным. Также хорошо проверять свои вычисления при помощи калькулятора, разделяя числитель полученной дроби на знаменатель.
Алгебра. 7 класс
Конспект урока
Периодические десятичные дроби. Периодичность десятичного разложения обыкновенной дроби
Перечень рассматриваемых вопросов:
Понятие бесконечной периодической десятичной дроби.
Примеры бесконечной периодической десятичной дроби.
Представление рационального числа в видебесконечной периодической десятичной дроби.
Любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число
преобразуется в положительную дробь.
Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Если в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
На прошлом уроке мы рассмотрели условия, при которых обыкновенную дробь можно представить в виде конечной десятичной.
А как поступать, когда невозможно представить её в таком виде?
Введём понятие бесконечной периодической десятичной дроби.
Если знаменатель q несократимой дроби p/q не имеет делителей, кроме 2 и 5, то эта дробь преобразуется в конечную десятичную дробь.
Если знаменатель содержит, кроме 2 и 5, другие простые делители, то мы не сможем представить её конечной десятичной дробью.
Знаменатель 9 = 3 3
5/9 не преобразуется в конечную десятичную дробь. Убедимся в этом, выполнив деление уголком.
Разделим числитель 5 на знаменатель 9.
Процесс деления в столбик бесконечный. Приходим к выражению 0,555…,
точки означают, что цифра 5 периодически повторяется бесконечно много раз.
Выражение 0,555… называют бесконечной периодической десятичной дробью или коротко: периодической дробью.
Читают: « ноль целых и пять в периоде».
Цифру (5) называют периодом дроби 0,(5).
Говорят, что число пять девятых представлено в виде периодической дроби ноль целых и пять в периоде.
Выражение 5/9 и 0,(5) являются обозначениями одного и того же числа в виде обыкновенной дроби 5/9 и в виде периодической дроби 0,(5).
Рассмотрим ещё пример.
Дробь четыре пятнадцатых несократимая, и её знаменатель имеет простые делители 3 и 5, поэтому деление не может быть конечным. Проверим.
Делим уголком 4 на 15.
читают: «ноль целых две десятых и шесть в периоде».
В примерах мы увидели разные периодические дроби.
Периодические дроби бывают двух видов: «чистые» и «смешанные».
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
Если применить правило деления уголком к любой несократимой дроби p/q
Где q – знаменатель, который, кроме 2 и 5 имеет другие простые делители, то получится бесконечная периодическая десятичная дробь, или коротко: периодическая дробь.
Приписывая к конечной десятичной дроби бесконечно много нулей, мы её приводим в бесконечную периодическую десятичную дробь с периодом 0.
45 = 45,0 = 45,000… = 45,(0)
0,673 = 0,673000 = 0,673(0).
Значит, любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число p/q преобразуется в периодическую дробь.
Верно обратное. Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа p/q.
Периодичность десятичного разложения обыкновенной дроби
Рассмотрим произвольную положительную несократимую дробь p/q
Покажем, что если разделить числитель дроби на знаменатель уголком, то в частном получится либо конечное, либо бесконечное периодическое её преобразование.
Нам известно, чтобы получить конечное десятичное разложение, знаменатель qне должен иметь простых делителей, кроме 2 и 5
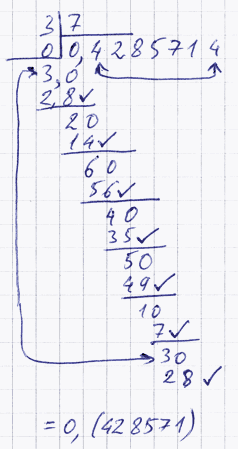
В других случаях может быть только бесконечное десятичное разложение, которое является периодическим. Пусть нужно найти десятичное разложение несократимой дроби 15/13.
Будем делить уголком 15 на 13.
Здесь одной звёздочкой отмечен этап вычислений, когда снесена последняя цифра делимого. Получаемые после этого остатки заключены в прямоугольники. Видно, что остатки, отмеченные двумя, тремя звёздочками, равны между собой. Это показывает, что процесс деления носит периодический характер и приводит к бесконечной периодической десятичной дроби, то есть:
Теперь на примере рассмотрим, как можно, зная бесконечную периодическую десятичную дробь, записать её обыкновенной дробью.
Запишем периодическую дробь 0,(7) в виде обыкновенной.
Для этого обозначим искомую величину х. Тогда справедливо равенство
Умножим это равенство на 10, получим
Вычтем из равенства (2) равенство (1).
Применив к дроби 7/9 деление уголком. Снова получим периодическую дробь 0, (7.)
Разбор заданий тренировочного модуля.
Подберите обыкновенную дробь, равную периодической десятичной 0,(14).
Варианты ответов: 14/99, 14/98 14/90
Обозначим искомую величину х. Тогда справедливо равенство:
Умножим это равенство на 100, получим
Вычтем из равенства (2) равенство (1).
Найдите десятичное разложение обыкновенной дроби 769/4950
Решение: Для решения задачи нужно выполнить деление уголком: