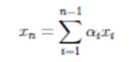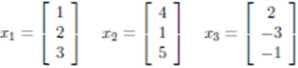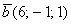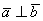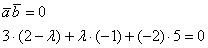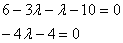Что значит ортогональные векторы
Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Как решить?
Находим скалярное произведение данных векторов:
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
Примеры пространственных задач на ортогональность векторов
Как решить?
Находим скалярное произведение данных векторов:
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
Ортогональность векторов. Перпендикулярность векторов.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
 |
| рис. 1 |
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Найдем скалярное произведение этих векторов:
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Найдем скалярное произведение этих векторов:
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = < ax ; ay ; az > и b = < bx ; by ; bz >, условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Линейная алгебра для исследователей данных
«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
kdnuggets
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
TimoElliott
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
TimoElliott
Область значений и нуль-пространство матрицы
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
Ортогональные векторы евклидова пространства и их свойства
Свойства ортогональных векторов
1. Нулевой вектор ортогонален каждому вектору пространства.
2. Взаимно ортогональные ненулевые векторы линейно независимы.
В самом деле, пусть векторы [math]\mathbf
Умножим обе части равенства скалярно на вектор [math]\mathbf
3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.
5. Если вектор [math]\mathbf[/math] ортогонален подмножеству [math]M[/math] евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. [math]\mathbf\perp M
6. Если [math]\mathbf
Это утверждение является обобщением теоремы Пифагора.
Процесс ортогонализации Грама-Шмидта
Рассмотрим следующую задачу. Дана линейно независимая система [math]\mathbf
1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:
а) [math]\mathbf
Поэтому в данном случае формулы вычисления коэффициентов [math]\alpha_
В остальном процесс ортогонализации остается неизменным.
4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы [math]\mathbf
Пример 8.18. Даны системы векторов евклидовых пространств:
а) [math]x=\begin
p_3(x)=x^2[/math] — элементы пространства [math]C[-1;1][/math] со скалярным произведением (8.28):
Провести ортогонализацию данных векторов.
Решение. а) Заметим, что система векторов [math]x,\,y,\,z[/math] линейно зависимая, так как [math]x[/math] и [math]y[/math] пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.
Получили ортогональные многочлены [math]q_1(x)=1,
1.6.7. Как проверить векторы на ортогональность?
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю, что векторы 
и 
ортогональны тогда и только тогда, когда 
. В координатах данный факт запишется следующим образом:
(для векторов плоскости);
(для векторов пространства).
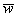
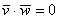
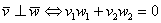
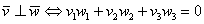
Задача 24
а) Проверить ортогональность векторов: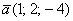 
и 
б) Выяснить, будут ли перпендикулярными отрезки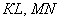 
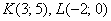
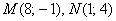
, если 
, 
.
Решение:
а) Выясним, будут ли ортогональны пространственные векторы. Для этого вычислим их скалярное произведение: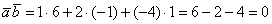 
, следовательно, 
б) Здесь речь идёт об обычных отрезках плоскости. Отрезки обычные, а задача всё равно решается через векторы. Найдём векторы: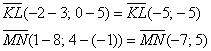 
и вычислим их скалярное произведение: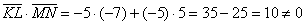 
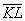
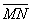
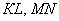
, следовательно, векторы 
и 
не перпендикулярны, а значит, не перпендикулярны и отрезки 
.
Ответ: а)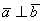 
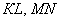
, б) отрезки 
не перпендикулярны.
Задача 25
Даны 4 точки пространства 
и 
. Выяснить будут ли перпендикулярными следующие прямые:
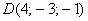
а)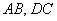 
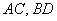
, б) 
.
Это задача для самостоятельного решения. По условию требуется проверить перпендикулярность прямых, а решаем снова через векторы – по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно: из ортогональности векторов автоматически следует перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.
Мощь аналитической геометрии – в векторах
Так, в рассмотренных задачах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета.
Завершая разговор об ортогональности, разберу ещё одну небольшую задачку, которая время от времени встречается на практике:
Задача 26
При каком значении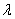 
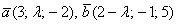
векторы 
будут ортогональны?
Решение: по условию требуется найти такое значение параметра 
, чтобы данные векторы были ортогональны. Два вектора пространства 
ортогональны тогда и только тогда, когда 
.
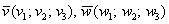
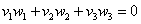
Дело за малым, составим уравнение: 
Раскрываем скобки и приводим подобные слагаемые: 
Решаем простейшее линейное уравнение: 
Ответ: при 
Здесь легко выполнить проверку, в исходные векторы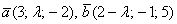 
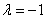
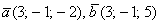
подставляем полученное значение параметра 
: 
и находим скалярное произведение:
– да, действительно, при 
векторы 
ортогональны, что и требовалось проверить.
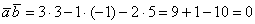
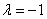
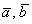
Простенький пример для самостоятельного решения:
Задача 27
При каком значении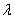 
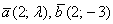
скалярное произведение векторов 
будет равно –2?
Едем дальше: