Что значит однородный стержень
Однородный стержень
Имеем однородный стержень длиной 
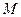
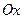
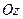
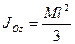
Момент инерции стержня относительно оси 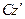
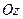
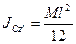
Эта тема принадлежит разделу:
Теоретическая механика
Воронежский государственный технический университет..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Однородный стержень
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Алгебраический момент силы относительно точки
Алгебраическим моментом силыотносительно точки называют произведение модуля силы на плечо силы относите
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 4). Момент сил
Пара сил и алгебраический момент пары сил
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны
Аксиомы статики
При формулировке аксиом предполагаем, что на твердое тело или материальную точку действуют силы, которые указаны в соответствующей аксиоме. I. Аксиома о равновесии системы двух сил
Простейшие теоремы статики
Теорема о переносе силы вдоль линии действия: Действие силы на твердое тело не изменится от переноса Теорема о трех силах: если твердое тело под действием трех сил
Приведение системы сил к простейшей системе. Условия равновесия
Лемма о параллельном переносе сил: силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту
Равновесие пар сил
Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных момент
Условия равновесия произвольной системы сил в векторной форме
Векторные условия равновесия произвольной системы сил: для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный
Условия равновесия пространственной системы сходящихся сил
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны н
Способы нахождения центра тяжести
Симметричные тела. Если тело имеет плоскость (ось, центр) симметрии, то его центр тяжести находится в этой плоскости (на оси, в центре).
Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы называют сосредоточенными. В действительности обычно силы бывают приложены к какой-либо
Трение скольжения
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения (трение первого рода). Пус
Трение качения
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает па
Кинематика точки
В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является
Скорость и ускорение точки
Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, ко
Кинематика твердого тела
Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тела относительно рассматриваемой системы отсчета. Движение твердого тела во мног
Поступательное движение твердого тела
Поступательным движением твердого тела называют такое его движение, при котором любая прямая, жестко скрепленная с телом, остается параллельной своему первоначальному положению в каждый моме
Вращение твердого тела вокруг неподвижной оси
Вращением твердого тела вокруг неподвижной оси (оси вращения) называется такое его движение, при котором точки тела, лежащие на оси вращения, остаются неподвижными в течение всего времени дв
Скорости и ускорения точек тела при вращении вокруг неподвижной оси
Известно уравнение вращения твердого тела вокруг неподвижной оси (рис. 29). Расстояние
Векторы угловой скорости и углового ускорения
Введем понятия векторов угловой скорости и углового ускорения тела. Если – единичный вектор оси вращения, напр
Векторные формулы для скоростей и ускорений точек тела
Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 32). Скорость точки по модулю и направлению можно представить векторным произведением
Сложное движение точки
Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее сложное движение точки. Во многих задачах движение точки приходится рассматривать относительн
Плоское (плоскопараллельное) движение твердого тела
Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, паралл
Скорости точек плоской фигуры
Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки фигуры, получаем
Ускорения точек плоской фигуры
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом
Мгновенный центр ускорений
В каждый момент движения плоской фигуры в своей плоскости, если и
Решение задач кинематики
Пример 3. Даны уравнения движения точки в плоскости :
Аксиомы динамики
I. Первая аксиома (законом классической механики, закон инерции): материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способност
Дифференциальные уравнения движения материальной точки
Используя основной закон динамики, можно получить дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить ди
Первая задача
Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат
Вторая задача
По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила
Центр масс
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры и
Сплошной диск
Имеем тонкий однородный диск радиусом и массой
Тонкое кольцо (круглое колесо)
Имеем тонкое кольцо радиусом и массой
Теоремы динамики
Внешними силами механической системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему. Внутренними силами механическ
Теорема о движении центра масс
Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к механической системе:
Количество движения точки и системы
Количеством движения материальной точки называют вектор, равный произведению массы точки
Теорема об изменении количества движения точки
Теорема об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе:
Теорема об изменении количества движения системы
Теорема об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на сис
Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рас
Теорема об изменении кинетического момента точки
Первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра:
Теорема об изменении кинетического момента системы
Первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.
Законы сохранения кинетических моментов
1. Если главный момент внешних сил системы относительно точки равен нулю, т. е.
Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Из теоремы об изменении кинетического момента (172′) следует дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Дифференциальные уравнения плоского движения твердого тела
Для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:
Работа силы
Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.
Кинетическая энергия
Кинетическая энергия точки и системы. Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е.
Теорема об изменении кинетической энергии точки
Теорема об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних си
Принцип Даламбера для материальной точки
Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики. Для несвободной точки он эквивалентен основному закону вместе с аксиомой связей. Уравнение движен
Принцип Даламбера для системы материальных точек
Рассмотрим систему материальных точек. К каждой точке системы в общем случае приложены равнодействующая актив
Силы инерции твердого тела в частных случаях его движения
При поступательном движении. Если твердое тело движется поступательно, то ускорения его точек одинаковы. Силы инерции этих точек составляют систему параллельных сил, направленных в од
Возможные перемещения
Для одной точки возможным (виртуальным) перемещением называется такое бесконечно милое (элементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на т
Элементарная работа силы на возможном перемещении. Идеальные связи
Элементарную работу силы на возможном перемещении ее точки приложения вычисляют по обычным формулам для элементарной работы, т.е.
Принцип возможных перемещений
Принцип возможных перемещений, или принцип Лагранжа, содержит необходимые и достаточные условия равновесия некоторых механических систем. Он формулируется следующим образом: для ра
Обобщенные координаты системы
Пусть система состоит из точек и, следовательно, ее положение в пространстве в каждый момент времени определя
Обобщенные силы
Запишем сумму элементарных работ сил, действующих на точки системы, на возможном перемещении системы:
Общее уравнение динамики
Общее уравнение динамики для системы с любыми связями (объединенный принцип Даламбера-Лагранжа или общее уравнение механики):
Уравнения Лагранжа второго рода
Уравнения Лагранжа можно рассматривать как алгоритм получения дифференциальных уравнений движения системы, т.е. дифференциальных уравнений относительно обобщенных координат. Уравнения Лагр
Решение задач динамики
Пример 7. На вертикальном участке
Библиографический список
1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607с. 2. Бутенин Н.В. Курс теоретической механики
Однородный стержень

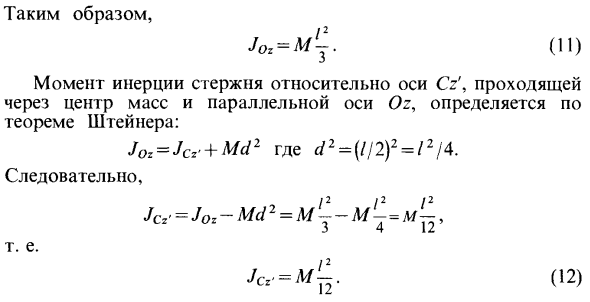
Однородный стержень
Значения RP для этих векторов считаются положительными, если направление соответствующего вектора соответствует выбранному полупрямому направлению, а отрицательное направление совпадает. Людмила Фирмаль
Поскольку dw = pdx, p = M / l — плотность стержня. При расчете интеграла это выглядит так Вот так JOl = M ^. (11). Момент инерции стержня относительно оси Cz ‘, проходящей через центр тяжести и параллельный оси Oz, определяется по теореме Штейнера. JOl = JCl + Md2, где rf2 = (// 2) 2 = / 2/4 так. Это JCz = m ‘^. (12)
Поэтому шестое уравнение системы, составленное путем решения этой задачи методом кинетостатики, по существу является дифференциальным уравнением для вращения твердых тел вокруг неподвижных осей. Людмила Фирмаль
Введем эти характеристики действия сил на твердые тела и рассмотрим их характеристики. Из определения алгебраического момента силы в некоторой точке следует, что она не зависит от переноса сил вдоль линии ее действия. Если линия действия силы проходит через точку момента, то алгебраический момент силы относительно точки равен нулю.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Что значит однородный стержень
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Обоснование. Стержень относительно системы отсчета, связанной с Землей, может либо двигаться поступательно, либо вращаться вокруг неподвижной оси. В инерциальной системе отсчета можно применить условие равновесия покоящегося тела, применив первый закон Ньютона. Стержень является однородным, т.е. имеет одинаковую плотность по всей длине. Поэтому центр тяжести стержня находится посередине. Для сил, линия действия которых не проходит через точку вращения (в данной задаче это точка опоры о пол), можно применить правило моментов.
Перейдем к решению.
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равна нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где — длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 30°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Обоснование. Стержень относительно системы отсчета, связанной с Землей, может либо двигаться поступательно, либо вращаться вокруг неподвижной оси. В инерциальной системе отсчета можно применить условие равновесия покоящегося тела, применив первый закон Ньютона. Стержень является однородным, т.е. имеет одинаковую плотность по всей длине. Поэтому центр тяжести стержня находится посередине. Для сил, линия действия которых не проходит через точку вращения (в данной задаче это точка опоры о пол), можно применить правило моментов.
Перейдем к решению.
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где l — длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Тонкий однородный стержень, частично погружённый в воду, удерживается в состоянии равновесия с помощью невесомой нерастяжимой нити (см. рис.). Длина отрезка АВ в два раза меньше длины отрезка ОА.
Выберите все верные утверждения.
1) Модуль силы натяжения нити меньше модуля действующей на стержень силы тяжести.
2) Сумма модулей силы натяжения нити и силы Архимеда больше модуля действующей на стержень силы тяжести.
3) Относительно оси, проходящей через точку О, плечо действующей на стержень силы тяжести меньше плеча силы Архимеда.
4) Относительно оси, проходящей через точку О, отношение плеча действующей на стержень силы Архимеда к плечу силы натяжения нити равно 1,2.
5) Относительно оси, проходящей через точку О, момент силы Архимеда больше момента действующей на стержень силы тяжести.
Изобразим на рисунке все силы, действующие на тело: сила натяжения, приложенная в точке О, сила тяжести, приложенная к середине стержня, сила Архимеда, приложенная к середине отрезка АВ.
1) Верно. По условию стержень находится в равновесии. Потому из условия равновесия тела следует:
или в проекции на вертикальную ось:
2) Неверно. Из предыдущего рассуждения следует, что T + FA = mg.
3) Верно. Плечо силы тяжести плечо силы Архимеда
Плечо силы Архимеда больше плеча силы тяжести.
4) Неверно. Относительно точки О плечо силы натяжения равно 0.
5) Неверно. Момент силы тяжести равен моменту силы Архимеда относительно точки О, т.к. стержень находится в равновесии.
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Обоснование. В упруго деформированных пружинах возникает сила упругости. Следовательно, к ней применим закон Гука. Система отсчета, связанная с Землей, является инерциальной. Стержень способен вращаться вокруг любой из точек подвеса. Так как стержень однородный, то на него кроме силы упругости действует сила тяжести, приложенная к середине стержня, вес груза. В инерциальной системе отсчета для вращающихся тел применимо правило моментов приложенных сил.
Перейдем к решению.
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной Если к этому стержню подвесить груз массой
на расстоянии
от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня M? Сделайте рисунок с указанием используемых в решении сил.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Обоснование. В упруго деформированных пружинах возникает сила упругости. Следовательно, к ней применим закон Гука. Система отсчета, связанная с Землей, является инерциальной. Стержень способен вращаться вокруг любой из точек подвеса. Так как стержень однородный, то на него кроме силы упругости действует сила тяжести, приложенная к середине стержня, вес груза. В инерциальной системе отсчета для вращающихся тел применимо правило моментов приложенных сил.
Перейдем к решению.
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Однородный стержень АВ массой m = 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль вертикальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль горизонтальной составляющей этой силы равен 0,3 Н? Трением пренебречь. Ответ укажите в ньютонах с точностью до одного знака после запятой.
По третьему закону Ньютона сила, с которой стержень давит на сосуд в точке B, равна силе, с которой сосуд действует на стержень в этой же точке. Найдём эту силу.
Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы: сила тяжести и силы со стороны стакана в точках С и В. Сила тяжести имеет только вертикальную составляющую, а значит, горизонтальные проекции сил в точках С и В должны компенсировать друг друга. Следовательно, величина проекции силы в точке С равна Из теоремы Пифагора найдём величину вертикальной проекции силы в точке С:
Рассмотрим теперь второй закон Ньютона для стержня в проекции на вертикальную ось: Отсюда получаем, что модуль вертикальной составляющей силы в точке B равен
Подскажите, пожалуйста, почему вертикальные составляющие сил, с которыми стержень давит на стенки сосуда в точках В и С имеют противоположное направление с силой тяжести? Стержень же давит на сосуд, значит, F(Cy) и F(Ву) должны совпадать с mg
Рассматриваются силы, приложенные к стержню. Стержень давит на сосуд, значит, сосуд действует на стержень силой реакции опоры.
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равна нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где
— длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 30°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где l — длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Почему силу F нельзя найти из уравнения (2), подставив туда силу Т, ведь Fх=Fcosа?
Сила не направлена вдоль стержня,
Сила натяжения нити приложена к концу стрежня, а сила тяжести — к его центру масс.
Тонкий однородный стержень, частично погружённый в воду, удерживается в состоянии равновесия с помощью невесомой нерастяжимой нити (см. рис.). Длина отрезка АВ в два раза меньше длины отрезка ОА.
Выберите все верные утверждения.
1) Модуль силы натяжения нити больше модуля действующей на стержень силы тяжести.
2) Сумма модулей силы натяжения нити и силы Архимеда меньше модуля действующей на стержень силы тяжести.
3) Относительно оси, проходящей через точку О, отношение плеча действующей на стержень силы тяжести к плечу силы натяжения нити равно 0,5.
4) Относительно оси, проходящей через точку О, плечо силы Архимеда больше плеча действующей на стержень силы тяжести.
5) Относительно оси, проходящей через точку О, момент силы Архимеда равен моменту силы тяжести.
Изобразим на рисунке все силы, действующие на тело: сила натяжения, приложенная в точке О, сила тяжести, приложенная к середине стержня, сила Архимеда, приложенная к середине отрезка АВ.
1) Неверно. По условию стержень находится в равновесии. Потому из условия равновесия тела следует:
Откуда следует, что T Ответ: 45.
Аналоги к заданию № 24094: 24147 Все
По П-образному проводящему проводнику, находящемуся в однородном магнитном поле, перпендикулярном плоскости проводника, скользит проводящий стержень (см. рисунок). На графике приведена зависимость ЭДС индукции, возникающей в стержне при его движении в магнитном поле. Пренебрегая сопротивлением контура и стержня, выберите все верные утверждения о результатах этого опыта. Известно, что модуль индукции магнитного поля равен В = 0,2 Тл, длина проводника l = 0,15 м, изменением сопротивления контура R пренебречь.
1) Стержень сначала двигался равноускоренно, а затем равномерно.
2) Через 2 с скорость стержня была равна 10 м/с.
3) В момент времени 4 с сила Ампера на стержень не действовала.
4) В промежуток времени от 2 с до 6 с сила тока в стержне не изменялась.
5) Через 6 с стержень остановился.
ЭДС индукции равна Таким образом, по графику
можно определить скорость стержня:
Сила тока в проводнике постоянна и равна
1) Стержень сначала двигался равноускоренно, а затем равномерно.
2) Через 2 с скорость стержня была равна
3) В момент времени 4 с в стержне течёт ток, и, значит, на него действует сила Ампера.
4) В промежуток времени от 2 с до 6 с сила тока в стержне не изменялась.
5) Через 6 с стержень двигался с ненулевой скоростью.
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Невесомый стержень АВ с двумя малыми грузиками массами m1 = 200 г и m2 = 100 г, расположенными в точках C и B соответственно, шарнирно закреплён в точке А. Груз массой M = 100 г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол а нить составляет угол с вертикалью, равный
Расстояние АС = b = 25 см. Определите длину l стержня АВ. Сделайте рисунок с указанием сил, действующих на груз M и стержень.
1. Систему отсчёта, связанную с Землёй, считаем инерциальной. Введём декартову систему координат хОу, как показано на рисунке. Поскольку груз находится в равновесии, согласно второму закону Ньютона
2. На стержень с грузами m1 и m2 действуют силы и
а также сила натяжения нити
Поскольку нить невесома, то
Кроме того, на стержень действует сила
со стороны шарнира. Запишем условие равенства нулю суммы моментов этих сил относительно оси вращения, проходящей через точку А — точку шарнирного закрепления стержня:
3. Решая систему уравнений (1) и (2), с учётом получим:
Ответ:
Невесомый стержень АВ с двумя малыми грузиками массами m1 = 200 г и m2 = 100 г, расположенными в точках C и B соответственно, шарнирно закреплён в точке А. Груз массой M = 100 г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол а нить составляет угол с вертикалью, равный
Расстояние АС = b = 25 см. Определите длину l стержня АВ. Сделайте рисунок с указанием сил, действующих на груз M и стержень.
Какие законы Вы используете для описания равновесия системы тел? Обоснуйте их применение к данному случаю.
Обоснование. Шары и груз движутся поступательно, следовательно, их можно считать материальными точками.
На груз действуют сила натяжения и сила тяжести. В инерциальной системе отсчета, связанной с Землей, можно применить второй закон Ньютона.
На шар, помещенный в точку В, действую сила натяжения и сила тяжести. Так же для этого тела в инерциальной системе отсчета применим второй закон Ньютона. Нить по условию нерастяжима, следовательно, силы натяжения, действующие на груз и шар В, равны по модулю.
На палку АВ действуют сила натяжения нити, вес шара С, вес шара В. В инерциальной системе отсчета можно применить правило моментов.
Перейдем к решению.
1. Систему отсчёта, связанную с Землёй, считаем инерциальной. Введём декартову систему координат хОу, как показано на рисунке. Поскольку груз находится в равновесии, согласно второму закону Ньютона
2. На стержень с грузами m1 и m2 действуют силы и
а также сила натяжения нити
Поскольку нить невесома, то
Кроме того, на стержень действует сила
со стороны шарнира. Запишем условие равенства нулю суммы моментов этих сил относительно оси вращения, проходящей через точку А — точку шарнирного закрепления стержня:
3. Решая систему уравнений (1) и (2), с учётом получим:
Ответ:
Однородный тонкий стержень массой m = 1 кг одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную горизонтальную доску, образуя с ней угол α = 30°. Под действием горизонтальной силы доска движется поступательно влево с постоянной скоростью (см. рисунок). Стержень при этом неподвижен. Найдите
если коэффициент трения стержня по доске μ = 0,2. Трением доски по опоре и трением в шарнире пренебречь.
Какие законы Вы используете для описания равновесия системы тел? Обоснуйте их применение к данному случаю.
Обоснование. Движение доски поступательное. Следовательно, ее можно принять за материальную точку. В инерциальной системе отсчета для доски, движущейся равномерно, применим второй закон Ньютона. Сила трения действует и на доску, и на стержень. В инерциальной системе отсчета применим третий закон Ньютона.
На стержень действуют сила реакции опоры, сила натяжения шарнира, сила тяжести. В инерциальной системе отсчета применимо правило моментов для вращающегося тела.
Перейдем к решению. 1. В инерциальной системе отсчёта Оху, связанной с Землёй, доска движется поступательно с постоянной скоростью. Поэтому сумма проекций на ось Ох всех сил, приложенных к доске, равна нулю (рис. а):
2. На рис. б показаны все силы, приложенные к стержню. Силы реакции шарнира представлена горизонтальными и вертикальными составляющими: По третьему закону Ньютона
поэтому
3. По условию задачи стержень покоится, поэтому сумма моментов сил относительно оси шарнира А равна нулю. Обозначив длину стержня через L, запишем это условие:
4. Доска движется относительно стержня, поэтому сила трения является силой трения скольжения:
5. Подставив (3) в (2), получим уравнение
позволяющее найти реакцию доски:
Ответ:
К тонкому однородному стержню в точках 1 и 3 приложены силы и
Через какую точку должна проходить ось вращения, чтобы стержень находился в равновесии? Массой стержня пренебречь.
Чтобы стержень не вращался вокруг некоторой точки, полный момент всех внешних сил относительно этой точки должен быть равен нулю. Из этого условия и определим, через какую точку необходимо провести ось вращения. Поскольку у нас всего две силы, можно сразу заключить, что искомая точка находится слева от точки 3, иначе обе силы вращали бы рычаг по часовой стрелке, и не уравновешивали бы друг друга. Обозначим расстояние между любыми двумя соседними точками через а расстояние от точки 3 до искомой точки через
Тогда сила
вращает стержень против часовой стрелки и ее момент равен
Сила
вращает стержень по часовой, и ее момент равен
Приравнивая два момента и решая линейное уравнение, получаем, что
Следовательно, ось вращения нужно расположить в точке 4.
А как вы нашли чему равно F2*x и F1*(x+2l)? Не подскажете?
Они равны друг другу:
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой и сопротивлением
каждый. Расстояние между рельсами
а коэффициент трения между стержнями и рельсами
Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией
(см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь.
При движении стержней с разными скоростями изменение потока вектора магнитной индукции, пронизывающего контур, за промежуток времени определяется по формуле
что приводит к возникновению в контуре ЭДС индукции
(здесь мы пренебрегли самоиндукцией контура).
В соответствии с законом Ома для замкнутой цепи в контуре появился ток. Направление этого индукционного тока зависит от характера изменения магнитного потока. Учитывая, что оба стержня движутся равномерно (а значит, сумма действующих на каждый стержень сил равна 0, можно сделать вывод, что скорость первого стержня больше скорости второго. Следовательно, площадь контура увеличивается, а значит, магнитный поток увеличивается. Откуда по правилу Ленца определяем, что индукционный ток течет по часовой стрелке. В цепи два проводника соединены последовательно, поэтому сила тока в цепи равна
На проводники с током в магнитном поле действуют силы Ампера и
как показано на рисунке. Кроме этих сил, на каждый стержень действует тормозящая сила трения
Так как стержни движутся равномерно, сумма сил, приложенных к каждому стержню, равна нулю. На второй стержень действуют только сила Ампера и сила трения, поэтому
Отсюда: относительная скорость

