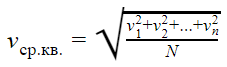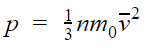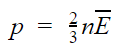Что значит одноатомный газ

Одноатомный газ

Одноатомный газ — это такой газ, в котором атомы не образуют химических связей друг с другом.

При стандартных давлении и температуре все инертные газы являются одноатомными. К инертным газам относятся: гелий, неон, аргон, криптон, ксенон и радон. Инертные газы с бо́льшими атомными массами могут создавать структурные образования, но более лёгкие являются нереактивными. При очень высоких температурах все химические элементы в газовом состоянии являются одноатомными.

Единственный вид движения молекул одноатомного газа — это поступательное движение (возбуждение электронов не является важным при комнатных температурах). Поэтому в адиабатном процессе одноатомные газы имеют идеализированный γ-фактор (C_p/C_v) равный 5/3, в то время как у идеальных двухатомных газов этот параметр равен 7/5. Молекулы двухатомного газа, помимо поступательного движения, могут ещё и вращаться (но вибрация при комнатных температурах для них недоступна).

Также про идеальные одноатомные газы можно сказать следующее:

молярная теплоёмкость при постоянном давлении (C_p) равна 5/2 R = 20.8 Дж *K −1 * моль −1 ; молярная теплоёмкость при постоянном объёме (C_v) составляет 3/2 R = 12.5 Дж* K −1 * моль −1 ;

Полезное

Смотреть что такое «Одноатомный газ» в других словарях:

одноатомный газ — vienatomės dujos statusas T sritis chemija apibrėžtis Dujos, kurių molekulėje yra tik vienas atomas. atitikmenys: angl. monoatomic gas rus. одноатомный газ … Chemijos terminų aiškinamasis žodynas

одноатомный газ — vienatomės dujos statusas T sritis fizika atitikmenys: angl. monatomic gas vok. einatomiges Gas, f rus. одноатомный газ, m pranc. gaz monoatomique, m … Fizikos terminų žodynas

Гелий — У этого термина существуют и другие значения, см. Гелий (значения). 2 Водород ← Гелий → Литий … Википедия

Аргон — 18 Хлор ← Аргон → Калий … Википедия

Радон — радиоактивный хим. элемент VIII гр. периодической системы, порядковый номер 86. Массовое число 222. Назв. элемента дано по наиболее долгоживущему изотопу Rn (Т = 3825 дням). В настоящее время известно 19 изотопов Р. с массовыми числами 204 и 206… … Геологическая энциклопедия

Криптон — У этого термина существуют и другие значения, см. Криптон (значения). 36 Бром ← Криптон → Рубидий … Википедия

СТАТИСТИЧЕСКАЯ ФИЗИКА — раздел физики, посвящённый изучению св в макроскопич. тел, т. е. систем, состоящих из очень большого числа одинаковых ч ц (молекул, атомов, эл нов и т. д.), исходя из св в этих ч ц и вз ствий между ними. Изучением макроскопич. тел занимаются и др … Физическая энциклопедия

Радон — У этого термина существуют и другие значения, см. Радон (значения). 86 Астат ← Радон → Франций … Википедия

Е939 — Гелий/Helium (He) Атомный номер 2 Внешний вид простого вещества инертный газ без цвета, вкуса и запаха Свойства атома Атомная масса (молярная масса) 4,002602 а. е. м. (г/моль) … Википедия

Эфир в физике — Содержание: 1) Э. до эпохи Декарта. 2) Э. картезианцев. 3) Э. Гюйгенса, Ньютона и позднейшего времени. 4) Свойства Э., как вида материи, согласно современным воззрениям. 5) Плотность Э. 6) Э. и тяготение. 7) Э. и молекулы обычных тел. 8) Инерция… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Идеальный газ

Газ: агрегатное состояние

У веществ есть три агрегатных состояния — твердое, жидкое и газообразное.

Их характеристики — в таблице:

Агрегатные состояния

Свойства

Расположение молекул

Расстояние между молекулами

Движение молекулы

Твердое

сохраняет форму и объем

в кристаллической решетке

соотносится с размером молекул

колеблется около положения в кристаллической решетке

Жидкое

близко друг к другу

молекулы малоподвижны, при нагревании скорость движения увеличивается

Газообразное

занимает предоставленный объем

больше размеров молекул

хаотичное и непрерывное

В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояний точно три?

На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Модель идеального газа

В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.

Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).

В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.

Свойства идеального газа

Среднеквадратичная скорость

Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.

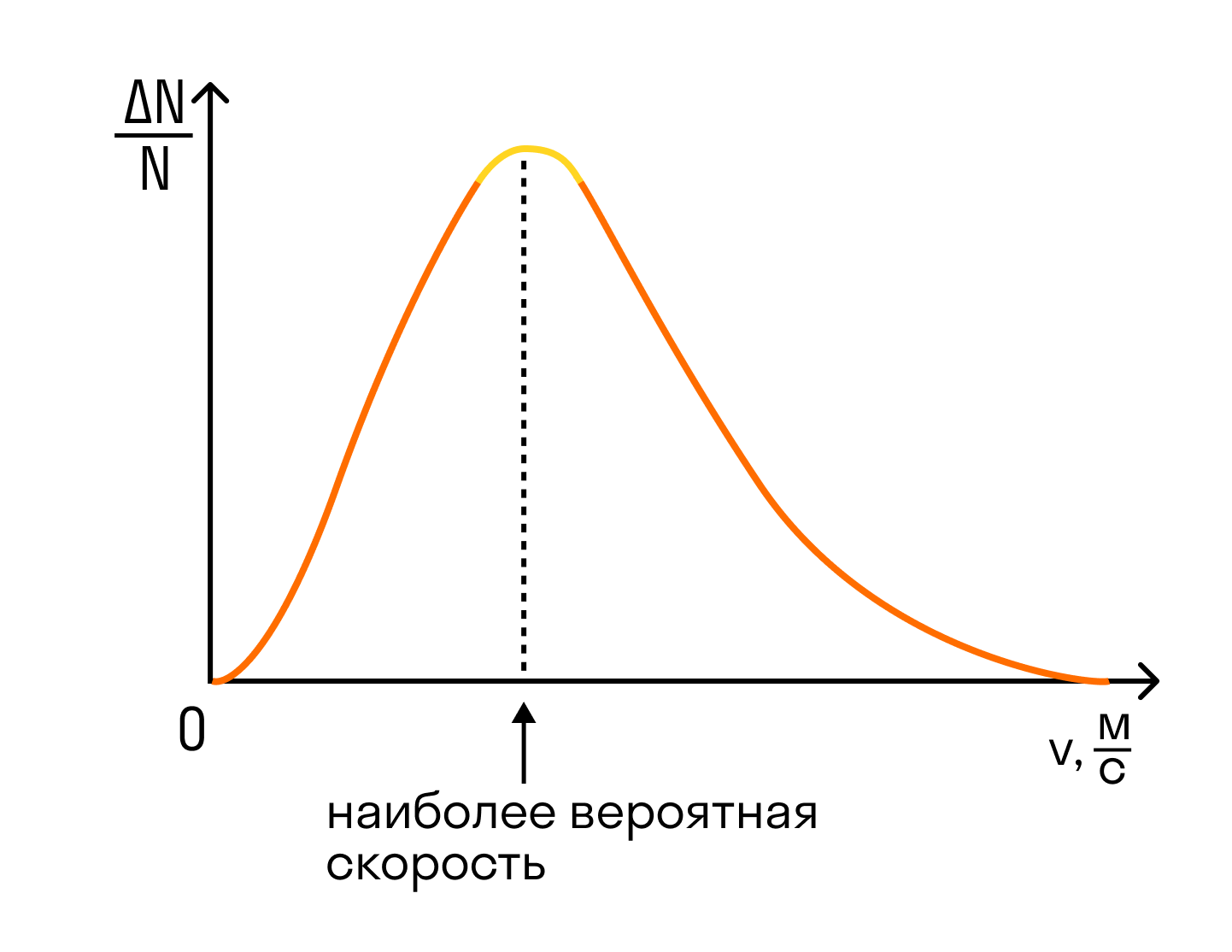
На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.

Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.

Средняя квадратичная скорость

v1, v2, vn — скорости разных молекул [м/с]

N — количество молекул [-]

Давление идеального газа

Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.

Эксперимент

Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление

p = F/S

F — сила [Н]

S — площадь [м2]

То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.

Рассмотрим аналогичный пример с двумя сосудами разной площади.

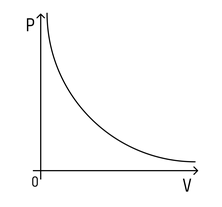
Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

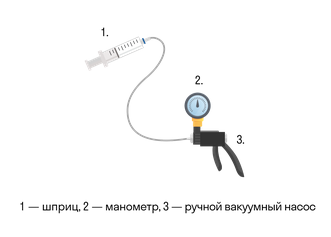
Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.

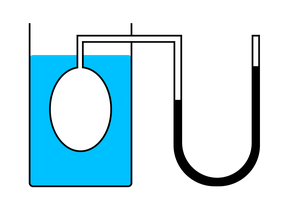
В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.

Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.

Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

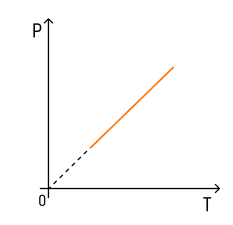
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:

Эта зависимость называется законом Шарля в честь ученого, открывшего ее.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ

p = nkT

p — давление газа [Па]

T — температура газа [К]

m 0 — масса одной молекулы [кг]

v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия

Е_к = mv 2 /2

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы

Е_к — средняя кинетическая энергия поступательного движения молекулы [Дж]

m₀ — масса молекулы [кг]

v — скорость молекулы [м/с]

Из этой формулы можно выразить m₀v 2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ

p — давление газа [Па]

n — концентрация [м-3]

E — средняя кинетическая энергия поступательного движения молекулы [Дж]

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

Источник

Что значит одноатомный газ

Полное вычисление свободной энергии (а с нею и остальных термодинамических величин) идеального газа требует конкретного вычисления статистической суммы, стоящей в аргументе логарифма в формуле (42,3)

Здесь представляют собой уровни энергии атома или молекулы (исключается кинетическая энергия поступательного движения частицы). Если производить суммирование лишь по всем различным уровням энергии, то надо учесть, что уровень может быть вырожденным, и тогда соответствующий член должен войти в сумму по всем состояниям столько раз, какова кратность вырождения. Обозначим последнюю посредством в этой связи кратность вырождения уровня часто называют его статистическим весом. Опуская для краткости штрих у напишем интересующую нас статистическую сумму в виде

Свободная энергия газа

Переходя к рассмотрению одноатомных газов, сделаем, прежде всего, следующее существенное замечание. По мере повышения температуры в газе увеличивается число атомов, находящихся в возбужденных состояниях, в том числе и в состояниях непрерывного спектра, соответствующих ионизации атома. При не слишком высоких температурах число ионизованных атомов в газе относительно совершенно ничтожно.

Существенно, однако, что газ оказывается практически полностью ионизованным уже при температурах, для которых Т порядка величины энергии ионизации (а не только при об этом § 104). Поэтому неионизованный газ имеет смысл рассматривать лишь при температурах, удовлетворяющих условию

Как известно, атомные термы (отвлекаясь от их тонкой структуры) располагаются таким образом, что расстояние от нормального до первого возбужденного уровня сравнимо по величине с энергией ионизации. Поэтому при температурах ион в газе будут практически отсутствовать не только ионизованные, но и возбужденные атомы, так что можно считать все атомы находящимися в нормальном состоянии.

Рассмотрим, прежде всего, простейший случай атомов, которые в своем нормальном состоянии не обладают ни орбитальным моментом, ни спином таковы, например, атомы благородных газов. При этом нормальный уровень не вырожден, и статистическая сумма сводится к одному члену: . Для одноатомных газов обычно полагают , т. е. отсчитывают энергию от нормального уровня атома; тогда . Разлагая логарифм в (45,2) на сумму нескольких членов, мы получим для свободной энергии выражение типа (43,1) с постоянной теплоемкостью

и химической постоянной

(О. Sackur, Н. Tetrode, 1912).

Полученное значение теплоемкости целиком связано с поступательными степенями свободы атома — по 1/2 на каждую степень свободы; напомним, что поступательное движение частиц газа всегда является квазиклассическим. «Электронные степени свободы» в данных условиях (отсутствие в газе возбужденных атомов), естественно, вообще не сказываются на термодинамических величинах.

Полученные выражения позволяют вывести критерий применимости статистики Больцмана. В этой статистике предполагаются малыми числа

(см. (37,1)). Достаточно, очевидно, потребовать выполнения условия

Для химического потенциала имеем из (43,3) со значениями из (45,3-4)

Поэтому получаем критерий

Это условие требует при заданной температуре достаточной разреженности газа. Подстановка численных значений обнаруживает, что фактически для всех атомарных (и молекулярных) газов это условие могло бы нарушиться лишь при таких плотностях, при которых становится существенным взаимодействие частиц, и газ уже все равно нельзя считать идеальным.

Полезно указать следующее наглядное истолкование полученного критерия. Поскольку большинство атомов обладает энергией порядка Т, а потому импульсом то можно сказать, что все атомы занимают в фазовом пространстве объем На этот объем приходится квантовых состояний. В больцмановском случае это число должно быть велико по сравнению с числом N частиц, откуда и получается (45,6).

Наконец, сделаем следующее замечание. Полученные в этом параграфе формулы на первый взгляд находятся в противоречии с теоремой Нернста: ни энтропия, ни теплоемкость не обращаются в нуль, при . Надо, однако, иметь в виду, что в тех условиях, в которых формулируется теорема Нернста, все реальные газы при достаточно низких температурах уже конденсируются. Действительно, теорема Нернста требует обращения в нуль при энтропии тела при заданном значении его объема.

Но при упругость насыщенного пара всех веществ становится сколь угодно малой, так что заданное конечное количество вещества в заданном конечном объеме не может оставаться при газообразным.

Если же рассмотреть принципиально возможную модель газа, состоящего из взаимно отталкивающихся частиц, то хотя такой газ не будет никогда конденсироваться, все равно при достаточно низких температурах перестанет быть справедливой статистика Больцмана; применение же статистики Ферми или Бозе приводит, как мы увидим ниже, к выражениям, удовлетворяющим теореме Нернста.

Источник