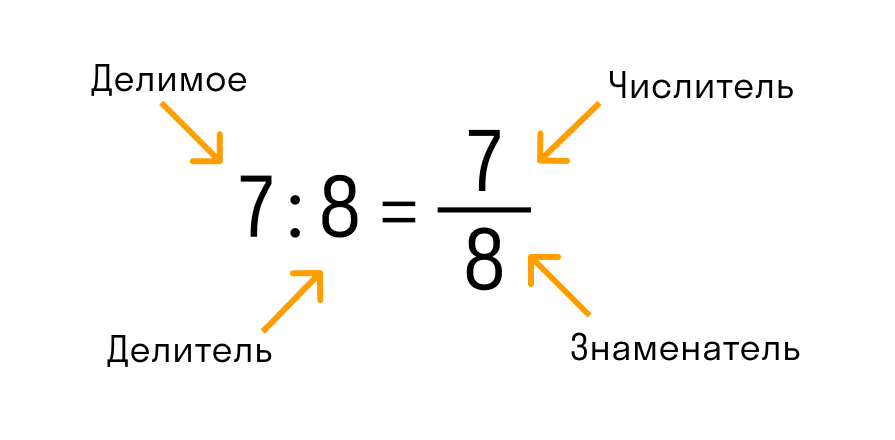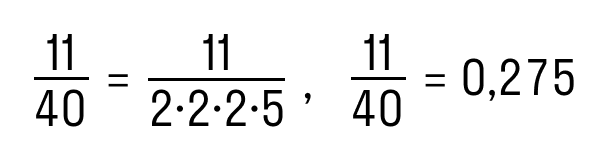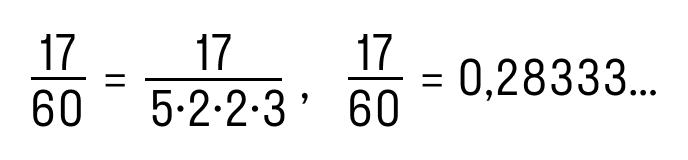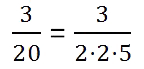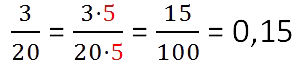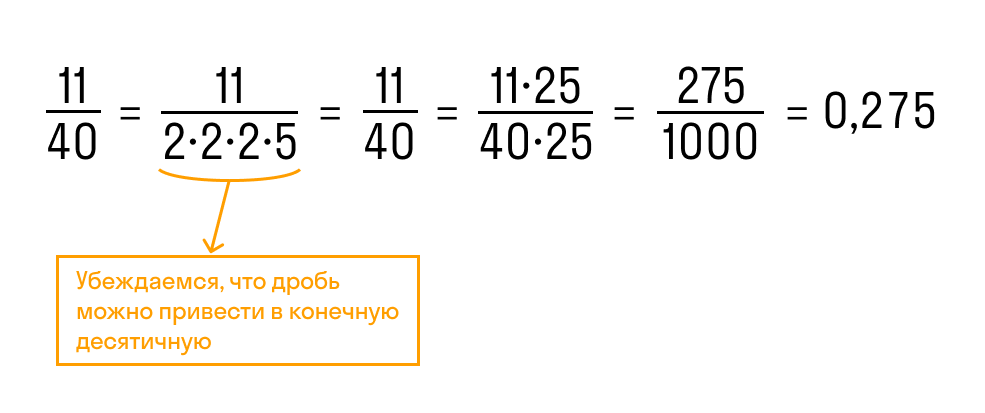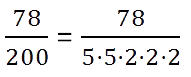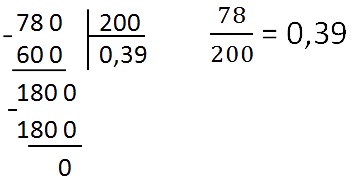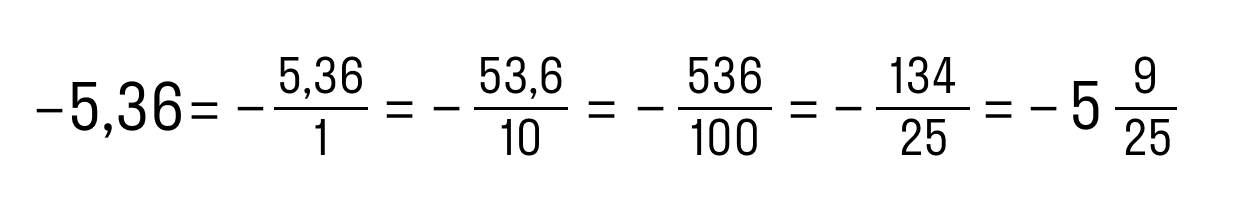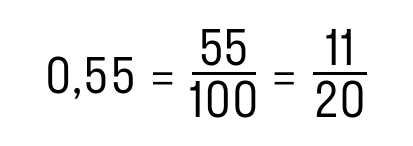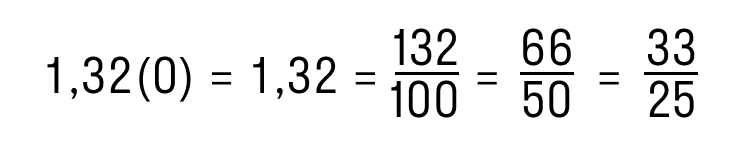Что значит обыкновенная дробь

Обыкновенные дроби

Вы будете перенаправлены на Автор24

Определение обыкновенной дроби

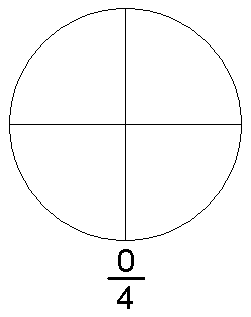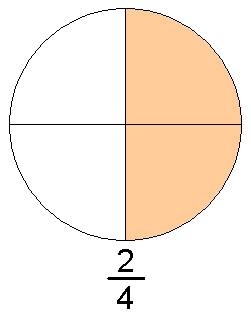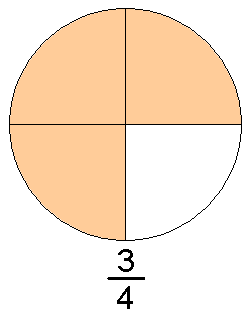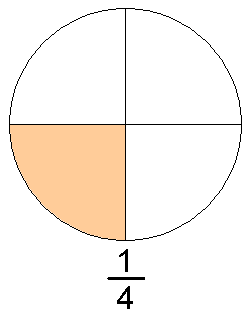
Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.

Приведем общее определение обыкновенной дроби.

Примеры обыкновенных дробей:

Числитель и знаменатель

Обыкновенная дробь состоит из числителя и знаменателя.

Готовые работы на аналогичную тему

Натуральное число как дробь со знаменателем 1

Дробная черта как знак деления

Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.

Равные и неравные обыкновенные дроби, сравнение дробей

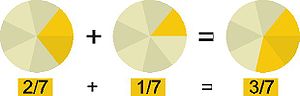
Результатом сравнения двух обыкновенных дробей может быть или их равенство, или их не равенство. При равенстве обыкновенных дробей их называют равными, в другом случае обыкновенные дроби называют неравными.

\[3\cdot 13\ne 17\cdot 4;\] \[39\ne 58.\]

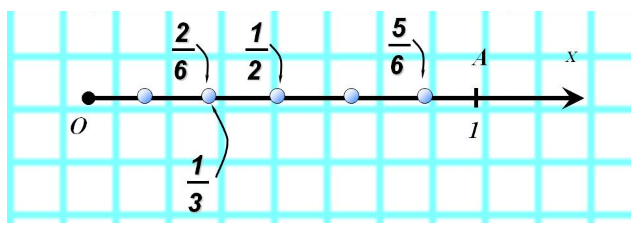
Дроби на координатном луче

Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче.

Чтобы отобразить на координатном луче дробное число, нужно единичный отрезок разделить на части.

Аналогично, точка с меньшей координатой будет лежать левее точки с большей координатой.

Источник

Доли, обыкновенные дроби, определения, обозначения, примеры, действия с дробями.

Эта статья про обыкновенные дроби. Здесь мы познакомимся с понятием доли целого, которое приведет нас к определению обыкновенной дроби. Дальше остановимся на принятых обозначениях для обыкновенных дробей и приведем примеры дробей, скажем про числитель и знаменатель дроби. После этого дадим определения правильных и неправильных, положительных и отрицательных дробей, а также рассмотрим положение дробных чисел на координатном луче. В заключение перечислим основные действия с дробями.

Навигация по странице.

Доли целого

Сначала введем понятие доли.

Предположим, что у нас есть некоторый предмет, составленный из нескольких абсолютно одинаковых (то есть, равных) частей. Для наглядности можно представить, например, яблоко, разрезанное на несколько равных частей, или апельсин, состоящий из нескольких равных долек. Каждую из этих равных частей, составляющих целый предмет, называют долей целого или просто долей.

Заметим, что доли бывают разные. Поясним это. Пусть у нас есть два яблока. Разрежем первое яблоко на две равные части, а второе – на 6 равных частей. Понятно, что доля первого яблока будет отличаться от доли второго яблока.

В зависимости от количества долей, составляющих целый предмет, эти доли имеют свои названия. Разберем названия долей. Если предмет составляют две доли, любая из них называется одна вторая доля целого предмета; если предмет составляют три доли, то любая из них называется одна третья доля, и так далее.

Одна вторая доля имеет специальное название – половина. Одна третья доля называется третью, а одна четверная доля – четвертью.

Понятие доли естественным образом распространяется с предметов на величины. Например, одной из мер измерения длины является метр. Для измерения длин меньших, чем метр, можно использовать доли метра. Так можно воспользоваться, например, половиной метра или десятой или тысячной долей метра. Аналогично применяются доли других величин.

Обыкновенные дроби, определение и примеры дробей

Для описания количества долей используются обыкновенные дроби. Приведем пример, который позволит нам подойти к определению обыкновенных дробей.

Пусть апельсин состоит из 12 долей. Каждая доля в этом случае представляет одну двенадцатую долю целого апельсина, то есть, . Две доли обозначим как , три доли – как , и так далее, 12 долей обозначим как . Каждую из приведенных записей называют обыкновенной дробью.

Теперь дадим общее определение обыкновенных дробей.

Обыкновенные дроби – это записи вида (или m/n ), где m и n – любые натуральные числа.

Числитель и знаменатель

Для удобства в обыкновенной дроби различают числитель и знаменатель.

Осталось обговорить смысл, заключенный в числителе и знаменателе обыкновенной дроби. Знаменатель дроби показывает, из скольких долей состоит один предмет, числитель в свою очередь указывает количество таких долей. Например, знаменатель 5 дроби 12/5 означает, что один предмет состоит из пяти долей, а числитель 12 означает, что взято 12 таких долей.

Натуральное число как дробь со знаменателем 1

Черта дроби как знак деления

Представление исходного предмета в виде n долей представляет собой не что иное как деление на n равных частей. После того как предмет разделен на n долей, мы его можем разделить поровну между n людьми – каждый получит по одной доле.

Равные и неравные обыкновенные дроби, сравнение дробей

В результате сравнения двух обыкновенных дробей получается один из результатов: дроби либо равны, либо не равны. В первом случае мы имеем равные обыкновенные дроби, а во втором – неравные обыкновенные дроби. Дадим определение равных и неравных обыкновенных дробей.

Источник

Обыкновенная дробь

Содержание

Терминология

Формальное определение

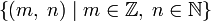
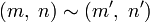
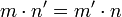
Формально рациональные числа определяются как множество классов эквивалентности пар по отношению эквивалентности , если . При этом операции сложения и умножения определяются следующим образом:

Связанные определения

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной.

Например, дроби , и — правильные дроби, в то время как , и — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби.

Например, 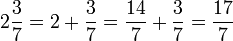. В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.

Комментарий

Термин дробное число (дробь) иногда используется как синоним к термину рациональное число, а иногда синоним любого нецелого числа. В последнем случае, дробные и рациональные числа являются разными вещами, так как тогда нецелые рациональные числа — всего лишь частный случай дробных.

Свойства

Основные свойства

Рациональные числа удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел. [1]

Дополнительные свойства

Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.

Счётность множества

Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, т. е. устанавливает биекцию между множествами рациональных и натуральных чисел.

Полученная таблица обходится «змейкой» по следующему формальному алгоритму.

Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.

В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. Т. е. дроби 1 / 1 ставится в соответствие число 1, дроби 2 / 1 — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.

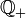
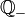
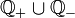
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел тоже счётно. Их объединение также счётно по свойству счётных множеств. Множество же рациональных чисел тоже счётно как объединение счётного множества с конечным.

Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, т. к. на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.

Недостаточность рациональных чисел

Рациональными числами вида 1 / n при больших n можно измерять сколь угодно малые величины. Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния. Легко показать, что это не верно.

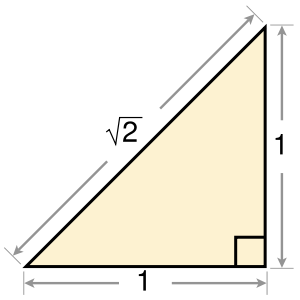
Из теоремы Пифагора известно, что гипотенуза прямоугольного треугольника выражается как квадратный корень суммы квадратов его катетов. Т. о. длина гипотенузы равнобедренного прямоугольного треугольника с единичным катетом равна 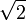, т. е. числу, квадрат которого равен 2.

Из вышесказанного следует, что существуют отрезки на плоскости, а, значит, и на числовой прямой, которые не могут быть измерены рациональными числами. Это приводит к необходимости расширения понятия рациональных чисел до вещественных.

Источник

Как перевести дробь в десятичную и наоборот

Что такое дробь: понятие

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.

Что такое десятичная дробь

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

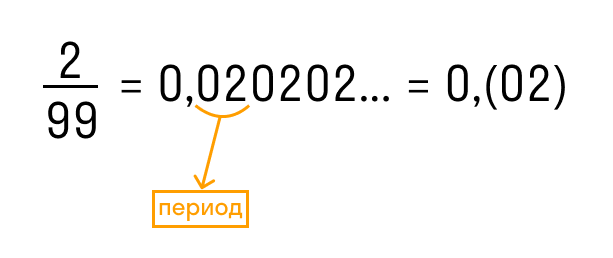
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Как перевести обычную дробь в десятичную

Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.

Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:

Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.

Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.

А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.

Способ 1. Превращаем знаменатель в 10, 100 или 1000

Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.

Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.

Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.

Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.

Способ 2. Делим числитель на знаменатель

Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.

Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.

Делим столбиком числитель на знаменатель — преобразование готово:

Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).

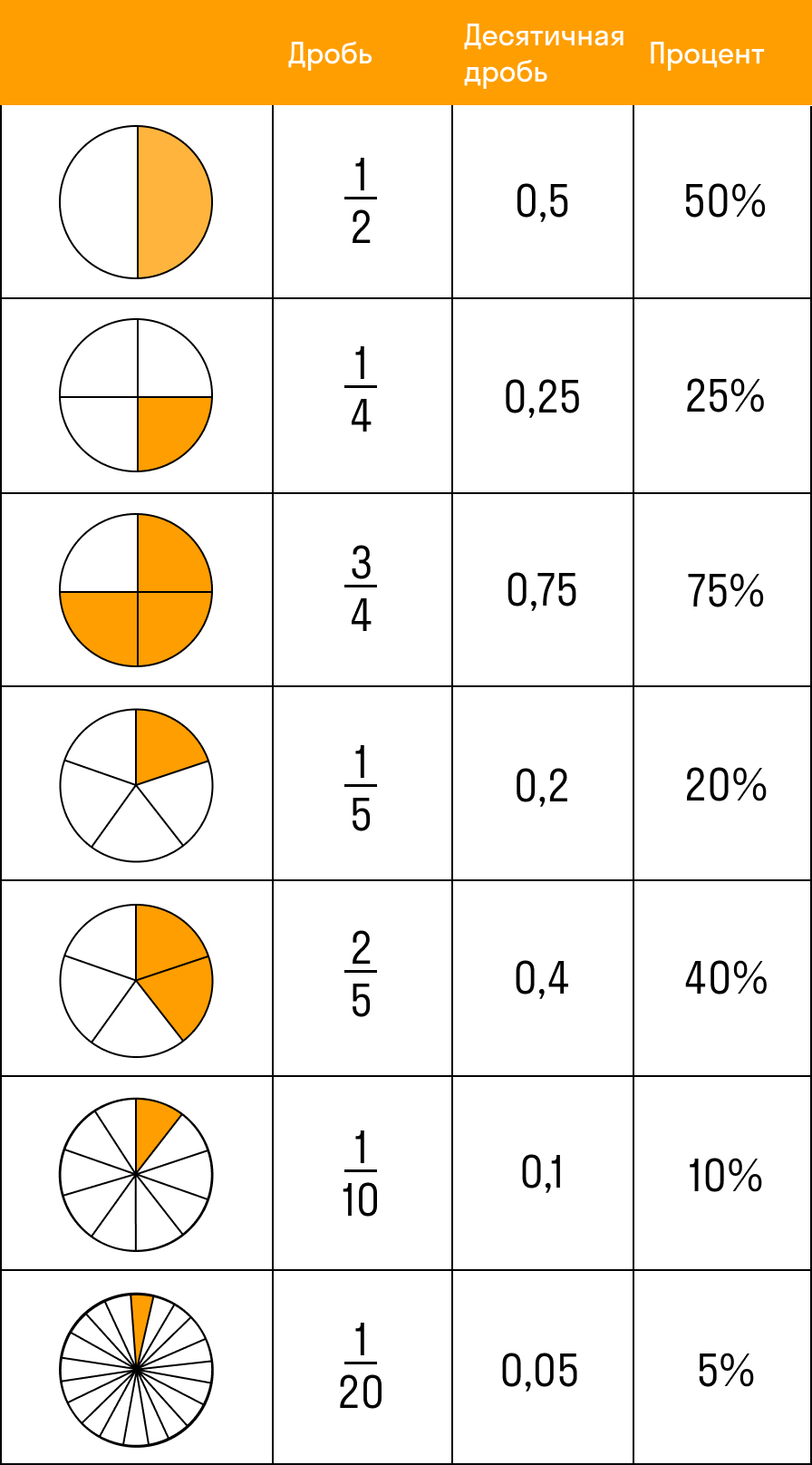
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!