Что значит нулевые числа
Нулевое число (0)
Определение нулевого числа
Когда на столе 2 яблока и мы берем 2 яблока, мы можем сказать, что на столе нет яблок.
Нулевое число не является положительным и отрицательным числом.
Ноль также является цифрой-заполнителем в других числах (например: 40,103, 170).
Нулевая цифра
При написании чисел нулевая цифра используется в качестве заполнителя.
204 = 2 × 100 + 0 × 10 + 4 × 1
История нулевых номеров
Кто придумал нулевое число?
Современный символ 0 был изобретен в Индии в VI веке, позже использовался персами и арабами, а затем и в Европе.
Символ нуля
В арабской системе счисления используется символ ٠.
Свойства с нулевым числом
x представляет любое число.
| Операция | Правило | пример |
|---|---|---|
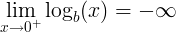 | ||
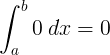 |
Нулевое дополнение
Сложение числа плюс ноль равно числу:
Нулевое вычитание
Вычитание числа минус ноль равно числу:
Умножение на ноль
Умножение числа на ноль равно нулю:
Число деленное на ноль
Деление числа на ноль не определено:
x ÷ 0 не определено
5 ÷ 0 не определено
Ноль делится на число
Деление нуля на число равно нулю:
Число в нулевой степени
Степень числа, возведенного в ноль, равна единице:
Логарифм нуля
Логарифм нуля по основанию b не определен:
Нет числа, с которым мы могли бы поднять основание b до нуля.
Только предел логарифма x по основанию b, когда x сходится к нулю, равен минус бесконечности:
Наборы, содержащие ноль
| Установить | Установить обозначение членства |
|---|---|
| Натуральные числа (неотрицательные) | 0 ∈ ℕ 0 |
| Целые числа | 0 ∈ ℤ |
| Вещественные числа | 0 ∈ ℝ |
| Сложные числа | 0 ∈ ℂ |
| Рациональное число | 0 ∈ ℚ |
Набор четных чисел:
Набор нечетных чисел:
Ноль является членом набора четных чисел:
Есть два определения набора натуральных чисел.
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
У целых чисел есть три определения:
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора целых чисел и набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
Ноль входит в набор целых чисел:
Является ли ноль рациональным числом?
Ноль можно записать как частное двух целых чисел.
Положительное число определяется как число больше нуля:
Поскольку ноль не больше нуля, это не положительное число.
Число 0 не является простым числом.
Ноль не является положительным числом и имеет бесконечное количество делителей.
Математика с нуля: чем интересно число 0?
Попробуем делить на ноль и узнаем больше об истории и свойствах числа, расположенного ровно посередине числовой оси.
Ноль — это, пожалуй, первое в нашей жизни загадочное число. Мы много слышали, например, о чудесах числа Пи, но мало кто имеет с ним дело в повседневной жизни. Не говоря уже о комплексных числах. А вот с нолём мы сталкиваемся повсюду: даже на клавиатуре обозначающая его цифра завершает ряд.
Но любой понимает, что с этим числом не всё в порядке. В детстве, когда мы ещё думали, что арифметика нужна только для счёта, нам объясняли, что ноль — это отсутствие. И это было странно.
Читайте также :
Поэтому и в истории человечества это число появилось поздно. Торговцы активно использовали счёт, но продавать, например, «ноль овец» не имело смысла. Впрочем, как и отрицательное их количество.
Вышло любопытно: например, древние греки не использовали ноль в принципе, зато уже знали об иррациональных числах, таких как √2. Это было связано с их любовью к геометрии: если у прямоугольного треугольника стороны будут равны 1, длина гипотенузы вычисляется как √2.
Но как же десятеричная система счёта? Ведь даже чтобы записать «10», нам нужен ноль. Но здесь дело только в записи числа: если вы вспомните римские цифры, то поймёте, что десятку можно представить и как Х. Конечно, такая форма была не особенно удобной, но даже вавилоняне, пользовавшиеся позиционной системой счисления (то есть, близкой нашей, а не древнеримской), долго обходились без ноля. Некоторое время его просто не было: числа, скажем, 36 и 306 не различались по написанию и определялись по контексту. Потом его роль стали выполнять два клинышка, вроде вот этих: 3’’6. Но и тогда они самостоятельной роли не играли — не было числа «ноль».
Сложно сказать, когда оно в действительности появилось. При этом есть свидетельства, что в Индии его использовали еще до нашей эры, после чего его переняли арабы — а вот на Западе оно стало входить в практику только в XIII веке усилиями итальянского математика Леонарда Фибоначчи. И то, его любовь к арабскому счислению долго не воспринималась всерьёз.
Известно, что первые слова, обозначавшие количество, имели конкретное применение — «пять лошадей» и «пять лодок» были для древнего человека разными категориями. Чтобы изобрести ноль, требовалось перейти на новый уровень абстрактного мышления.
Но если мы поверим в ноль, его свойства поразят воображение.
Возвести в нулевую степень
Ещё по этой теме :
С самыми простыми операциями проблем не возникает: прибавить ноль или вычесть его из числа — число остаётся тем же, умножить на ноль — получится ноль… Всё это укладывается в рамки здравого смысла. Сложнее становится при возведении в нулевую степень. В школе сообщают, что результатом в каждом случае будет единица. Откуда она взялась?
Тут рассудок уже пасует. Степень — это, как известно, то, сколько раз мы берём число как множитель самого себя.
Если степень нулевая, число не является множителем ни разу, но… как из этой пустоты «родилась» единица?
Чаще всего в школе этот вопрос решается догматически: на объяснения не остаётся желания и сил. А ведь именно здесь пролегает одна из границ, за которой простая арифметика, наглядно показываемая на яблоках и прочих исчислимых вещах, становится уже чистой и прекрасной абстракцией.
Вспомним правила обращения с числами, возводимыми в степень, и представим себе следующий пример:
В отношениях с одинаковыми основаниями степеней мы можем делать следующее:
Так вот чудесным образом, благодаря только принятию ноля как числа, мы переходим к новому странному открытию, и математика совершает куда более далёкий прыжок от реальности, чем просто представление «у меня ноль конфет».
Но именно внутренняя логика системы, которая может быть понята умом, но не может быть представлена в вещественном мире — это и есть красота абстракции.
Поделить на ноль
Это может быть интересно :
«Деление на ноль» давно стало интернет-мемом, правда, довольно неопределённым. То оно означает аннигиляцию чего бы то ни было (а ведь логичнее было бы умножить на ноль), то вовсе разрушение математических основ мироздания. И второе ближе к истине.
Большинство учёных всё-таки считают эту операцию с нолём невозможной или обладающей неопределённым результатом.
В чём же дело, и почему даже машины не могут между собой «договориться»?
Чисто арифметически делимость на ноль приводит к рискованным выводам. Смотрите сами:
Это лишь известное нам свойство ноля. Но если на него можно делить, то, сократив обе части, мы получим:
Почему же речь иногда заходит о бесконечности? Дело в том, что проблему пытаются решить через деление на бесконечно малую функцию, то есть построение графика функции, где x стремился бы к нулю. Так мы пытаемся найти y = 1 / x, и получается следующее:
Кстати говоря, с делением ноля на ноль наблюдается ещё большее единодушие: тут, если мы соберёмся построить функцию, результаты могут быть практически какими угодно (0, ±1, ±∞…) В общем, ноль, оставаясь числом, снова подрывает основы математики, если мы нарушаем неприкосновенность его свойств.
Ноль — чётное число?
Это может быть интересно :
Если он так необычен (и не забываем, что он не является ни положительным, ни отрицательным), можно ли говорить о его чётности? Интуитивно мы догадываемся, что он чётный, ведь целые числа сменяют друг друга именно по такому принципу: 2 — чётное, 1 — нечётное, следующим должно быть снова чётное. Но странность ноля настораживает, подсказывает, что и в этом вопросе нужно держать ухо востро.
Какое главное требование он должен пройти в этом случае? Деление на двойку без остатка, и он выдерживает испытание с достоинством: 0/2=0. Получается целое число 0, причём сколько бы мы ни продолжали деление, результат будет получаться одинаковым — можно сказать, что он является «наиболее» чётным или «бесконечно» чётным числом.
Если быть более точным, мы должны взять другое определение с обратной операцией. Чётное число может быть представлено в виде 2x, где x — целое число, но и в таком случае всё просто: 0 = 2 ∙ 0.
Есть и такое свойство чётных чисел, что при сложении двух из них должно получаться снова чётное, проверим:
При всей необычности ноля даже его удивительное соответствие всем критериям кажется странным, не так ли?
Что смотреть и читать о ноле?
Чтобы узнать больше о ноле как одном из самых загадочных явлений математики, а также об истории его «открытия», вы можете обратиться к следующим ресурсам:
1. Numberphile. Это популярнейший в среде любителей математики Youtube-канал, у которого уже более чем 1,5 миллиона подписчиков. Есть видео и о ноле, которые в переводе на русский можно найти здесь.
2. Книга Чарльза Сейфе «Ноль. Биография опасной идеи». Автор, хоть и не без излишнего сгущения красок, рассказывает об истории ноля как числа и цифры — причем в обширном контексте истории науки, от Архимеда до теории струн. В качестве бонуса вы получите приложения с задачками, где используется ноль. Например, вам предложат доказать, что Уинстон Черчилль был морковкой, и построить машину времени из кротовой норы.
3. Сборник эссе, в которых фантаст Айзек Азимов рассказывает о том, как человек, переходя от счёта на пальцах ко всё более сложным вычислениям, разработал основные математические операции, а также о том, как числа связаны с нашим восприятием времени и пространства. Природе ноля и его парадоксам посвящена открывающая книгу статья «Nothing Counts».
Даже если вам не нравились в школе ни арифметика, ни алгебра, у вас всегда есть возможность ими заинтересоваться. Учить математику с нуля уже не получится — худо-бедно мы начали считать ещё дошколятами. А вот полюбить её с нуля — вполне реальная перспектива.
Ноль (число)
0 (ноль, нуль от лат. nullus — никакой) — число, обозначаемое цифрой ноль. Ноль — это нейтральный элемент для операции сложения (то есть при сложении с нулём число не меняется). Аналогичным свойством по умножению обладает единица. Умножение любого элемента множества на ноль даёт ноль. Деление на ноль невозможно, так как приводит к противоречию, — в самом деле если бы результатом деления числа 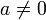
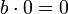
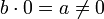
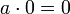
В зависимости от множества, на котором определена операция сложения, ноль может иметь различную природу. Обычно имеют в виду действительный ноль, то есть ноль в контексте множества действительных чисел; комплексный ноль; ноль-многочлен; ноль-вектор.
Действительный ноль является границей между областью положительных и областью отрицательных чисел. Ноль не имеет знака. Иногда множество действительных чисел разделяют на три подмножества: положительные, отрицательные и беззнаковые числа. При этом беззнаковые числа — множество, состоящее лишь из ноля. Множество беззнаковых чисел замкнуто относительно операций сложения и умножения. В Древней Греции число 0 известно не было.
Содержание
Ноль как натуральное число
Существуют два подхода к определению натуральных чисел, отличающиеся причислением нуля к натуральным числам. В российских школьных программах по математике не принято причислять ноль к натуральным числам.
В математике
В науке
В других областях
См. также
См. также
Ссылки
Полезное
Смотреть что такое «Ноль (число)» в других словарях:
Ноль — (нуль) (от лат. nullus никакой). Содержание 1 В математике 2 Наука и техника 3 Другие значения … Википедия
НОЛЬ — НОЛЬ, я и НУЛЬ, я, муж. 1. В математике: действительное число, от прибавления к рого никакое число не меняется. Сводиться к нулю (перен.: терять значение, превращаться в ничто). 2. Цифровой знак «0», обозначающий такое число, а также, в составе… … Толковый словарь Ожегова
ноль — • ноль и нуль сущ., м., употр. сравн. часто Морфология: (нет) чего? ноля и нуля, чему? нолю и нулю, (вижу) что? ноль и нуль, чем? нолём и нулём, о чём? о ноле, нуле; мн. что? ноли и нули, (нет) чего? нолей и нулей, чему? нолям и нулям, (вижу)… … Толковый словарь Дмитриева
ноль — без палочки, козявка, шишка на ровном месте, мыльный пузырь, пустое место, отставной козы барабанщик, шушваль, прыщ на ровном месте, мелкая сошка, не велика птица, десятая спица, миздрюшка, последняя спица в колеснице, маленький человек,… … Словарь синонимов
ноль — НОЛЬ, НУЛЬ, я; м. [от лат. nullus никакой] 1. Число, от прибавления (или вычитания) которого к любому числу последнее не меняется. Умножение на н. даёт в произведении н. // Цифровой знак 0. Напиши цифру н. 2. Условная величина, с которой… … Энциклопедический словарь
Число с плавающей запятой — Число с плавающей запятой форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную.… … Википедия
НОЛЬ — НОЛЬ, в математике число, от прибавления (или вычитания) которого к любому числу х последнее не изменяется: х+0=х. Умножение любого числа на нуль дает нуль. Деление на нуль невозможно. Понятие нуля не было известно древним грекам; оно проникло на … Научно-технический энциклопедический словарь
Ноль (цифра)
Ноль (нуль, от лат. nullus — никакой) — название первой (по порядку) цифры в стандартных системах исчисления, а также математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех левее стоящих цифр на разряд (например, в десятичной системе счисления, умножает на десять). Сравните, например, числа 410 и 4010; 416 и 4016 (нижний индекс означает основание системы счисления).
Содержание
История
В Индии
Индийцы называли знак, обозначающий отсутствие какого-либо разряда в числе, словом «сунья», что значит пустой (разряд, место, см. Шуньята). Арабы перевели это слово по смыслу и получили слово «сифр».
Первое достоверное свидетельство о записи нуля относится к 876 г.; в настенной надписи из Гвалиора (Индия) имеется число 270. Некоторые исследователи предполагают, что нуль быль заимствован у греков, которые ввели в качестве нуля букву «о» в шестидесятеричную систему счисления, употребляемую ими в астрономии.
Другие, наоборот, считают, что ноль пришёл в Индию с востока, он был изобретён на границе индийской и китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого кружка.
Индийцы вначале обозначали нуль точкой.
В Европе
Леонардо Пизанский (1228) употребил для передачи арабского термина «сифр» слово zephirum (латинское слово zephyrus — зефир означало западный ветер), а одновременно с ним другой главный поборник индийской нумерации в Европе, Иордан Неморарий (1237), употребляет арабскую форму cifra.
С начала XVI века в немецких руководствах слово «цифра» получает значение современное, слово «нуль» входит в повсеместное употребление в Германии и в других странах, сначала как слово чужое и в латинской грамматической форме, постепенно принимая форму, свойственную данному национальному языку.
В России
Ноль в других культурах
Майя использовали ноль в своей двадцатеричной системе счисления почти на тысячелетие раньше индийцев. Первая сохранившаяся стела с датой календаря майя датируется 7.16.3.2.13, 6 Бен 16 Шуль 10 декабря 36 года до н. э..
В империи инков Тауантинсуйу для записи числовой информации использовалась узелковая система кипу, основанная на позиционной десятеричной системе счисления. Цифры от 1 до 9 обозначались узелками определённого вида, ноль — пропуском узелка в нужной позиции. В современном кечуа ноль обозначается словом кечуа ch’usaq (букв. «отсутствующий», «пустой»), однако то, какое слово использовалось инками для обозначения нуля при чтении кипу, пока неясно, поскольку, например, в одних из первых кечуа-испанских (Диего Гонсалес Ольгин, 1608) словарях и первом аймара-испанском (Лудовико Бертонио, 1612) не было соответствия для испанского «cero» — «ноль».
Проект по математике «История числа 0»
МКОУ «Овсорокская СОШ»
ПРОЕКТ по математике
на тему : «История числа нуль»
Выполнил : ученик 5 класса
Руководитель : учитель математики
Сила в нём и красота.
Нуль всегда всё округляет
И на числа так влияет,
Что из хилой единицы
Десять может получиться,
Если шесть нулей добавить,
Нуль, как цифра, очень быстро.
Человек с ним не герой,
Тот, кто трусоват, ничтожен
Нуль без палочки, пустышка,
Неприметный, даже слишком.
Это хуже вражьих пуль.
Будь хотя бы единицей,
А за ней ставь вереницей
Несколько нулей подряд,
И тогда сам будешь рад,
Что не стал ты пуст и кругл,
Как тот одиночка нуль.
Рисовали просто круг
Получилась цифра вдруг
Эту цифру назовём
Круглым толстеньким нулём
Все считают от нуля.
Здесь чего-то нет совсем!
Изучить с точки зрения человеческого взгляда число 0 и выяснить почему возникла необходимость в нуле, показать значимость открытия этой цифры.
— изучить историю возникновения числа 0:
— изучить специфические свойства числа 0;
— выяснить применение числа 0 в других областях знаний, кроме математики;
— выяснить какое значение число 0 имеет в практической жизни людей;
— выяснить место нуля в литературном и народном творчестве.
Цифра вроде буквы О –
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит, ничегошеньки
люди всегда используют числа и цифры везде: в работе, в быту, на отдыхе. Да и счет – вещь важная и нужная. А многие люди ничего не знают о возникновении счета.
поиск и сбор информации из различных источников (научно-популярной литературы, сайтов сети Интернет)
Когда-то многие считали,
Что нуль не значит ничего
И, как ни странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел
Он все же место получил,
И все действительные числа
На два разряда разделил.
Нуль не в один из них не входит,
Он сам составил чисел класс,
О всех его особых свойствах
Мы поведем сейчас рассказ.
История нуля берёт своё начало с незапамятных времён. Кто первым догадался обозначить цифрой «ничто»? Мы никогда не узнаем. Можем только утверждать, что таких гениев было несколько.
Кто-то придумал знак для нуля в Древнем Вавилоне в 4 веке до н.э.. Но их изобретение не получило широкого распространения, потому что их математический аппарат базировался не на десятичной, а на 60-ричной системе счисления. Иными словами, в их математике было не 10, а 60 цифр. Зато из их математики мы взяли принципы учета времени — 60 минут по 60 секунд составляют 1 час. Нуль в представлении вавилонян изображался в виде двух поставленных наискось стрел и был не цифрой, а лишь знаком пробела.
В доколумбовой Америке индейцы Майя также пришли к понятию числа ноль, произошло это примерно в 5 веке нашей эры. Но так как их цивилизация была закрыта для посторонних и территориально обособлена, а впоследствии попросту исчезла, это изобретение снова было потеряно. Нуль у майя был не числом, а значком пробела и не участвовал в операциях сложения, вычитания, умножения и деления.
Интересны были различные способы обозначения чисел, придуманные египтянами и вавилонянами, греками и римлянами. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были всё новые и новые знаки. Величайший древнегреческий математик Архимед научился называть громадные числа, но обозначать их он не умел. Архимед, один из гениальнейших математиков в истории человечества, не додумался до…. нуля!
Изобретателем формы нуля можно считать великого греческого астронома Птолемея, так как в его текстах на месте знака пробела стоит греческая буква омикрон, очень напоминающая современный знак нуля. Но Птолемей использует нуль в том же смысле, что и вавилоняне.
Родиной настоящего нуля по праву считают Индию 6 век нашей эры. Итогом индийской математики стала запись любых чисел с помощью десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которыми мы пользуемся поныне
В Индии примерно полторы тысячи лет тому назад 0 был присоединён к девяти цифрам. Появилась возможность обозначать этими цифрами любое число, как бы велико оно не было. И самое главное, запись таких гигантских чисел стала довольно короткой. Именно индийские математики изобрели нуль во всех его трех смыслах. Например, индийский математик Брахмагупта еще в VII века н.э. активно стал использовать отрицательные числа и действия с нулем. Но он утверждал, что число, деленное на нуль, есть нуль, что конечно ошибка.
Индийской системой обозначений мы пользуемся до сих пор. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы узнали её от арабов. Поэтому наши цифры, в отличие от римских, стали называть арабскими
В центре Будапешта, неподалеку от одного из красивейших мостов, установлено каменное изваяние нуля. Цифра «0» и две буквы на пьедестале «КМ» означают начало всех дорог, нулевой километр, от которого ведется отсчет километров. «Нуль», как это сооружение иногда называют будапештцы, стал одной из достопримечательностей столицы Венгрии.
В Дунайском биосферном заповеднике есть место называемое «нулевым километром».
Так называется место, где Дунай впадает в Черное море и откуда начинается отсчет расстояний на реке. Даже соответствующий монумент имеется. Прогуляйтесь немного по пляжу рядом с «нулем».
Памятник числу «0» в Мюнхене
Число 0 пишется, как и буква «о».
До конца 19 века использовались нулевые меридианы.
0 число имеет два название нуль ноль.
Нулевая температура это минимальная температура всех тел во вселенной.
Новый день начнется после того как на электронных часах стоит четыре 0.
На Руси число 0 писала с палочкой внутри, отсюда и пошла поговорка ноль без палочки.
Жест пальцами на руках похожий на ноль, означает, что все хорошо.
Число 0 все привыкли считать самым малым из натуральных чисел, но число 0 стоит после девятки.
На число 0 в 1964 была придумана детская сказка «приключения нулика»
Слово «Цифра» — на арабском означает 0(ноль).
У большинства календарей не существует 0(нулевого) года, месяца, дня.
Значение нуля в жизни современного общества
2. Важное значение имеет ноль и по тому, что от него ведётся отсчёт.
3. Без ноля не существовало бы компьютерной техники.
4.Ноль – удобное обозначение начала пути
По железным дорогам России все расстояния считают от Москвы Так что Москва – это ноль на карте железных дорог, точка, из которой все начинается.
Взгляните на термометр. На нем нуль показывает температуру, при которой тает лед
Попав как множитель
Он сводит мигом всех на нет.
И потому в произведенье
Один за всех несет ответ
А относительно деления,
Во первых нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленье.
Противоречье в нем самом.
Значение числа в религиях мира
В религиях не так часто встречаются цифры. Но вот число 0 замечено в Коране и в Иудаизме. В Иудаизме рассказывается, что это число начало всего. С ноля все началось. Это число ноль напоминает яйцо, а яйцо — это жизнь. В Библии хорошо описывается этот момент, что после взрыва, когда все и все погибло, остались яйца животных ну и т д. В Коране тоже вспоминается о яйце, его также сравняют с числом ноль (0). Но в Коране пишется, что число ноль имеет точно такую форму, как и земля, и все живое начинается с яйца, которое также имеет форму как ноль.
Цифра ноль первая появилась в буддизме, и она означала пустоту.
Место нуля в литературном и народном творчестве.
Ноль без палочки» (прост.) – ничего не стоящий, не значащий человек;
«ноль внимания» – полное равнодушие, безразличие со стороны кого-либо к кому-либо или чему-либо
Существует загадка о нуле
Сколько лет в яйце цыпленку,
Сколько крыльев у котенка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра…
Детские стихи про цифру ноль:
Ноль похож на колобок,
Он пузат и круглобок.
На него похожа Кошка,
На горшке сидит король,
Ищет всюду цифру ноль.
Можем подсказать ответ:
Ноль – когда чего-то нет!
Ноль – задумчивый мудрец.
Где начало, где конец
Сам не может разобрать.
Как его нам не узнать!
Вы не встретите миногу,
Чтоб плыла в строю не в ногу.
Почему? Да, просто ног
Ровно НОЛЬ у рыб миног
А в строю-то им раздолье…
Ой, совсем забыл про ноль я!
Так его и нету, вроде,
Хоть и водится в природе.
Ноль не значит ничего.
Очень жалко мне его.
Он хороший: круглый, гладкий,
Всё с подсчётами в порядке.
Ноль со всеми очень дружен,
Он везде и всюду нужен.
Ноль не требует наград,
Завершает цифр ряд
Мне интересно было работать над этой темой. В процессе работы я много узнал интересного. Теперь я знаю историю возникновения числа нуль, некоторые свойства нуля, где можно применить число 0 в других областях знаний, кроме математики, какое значение число 0 имеет в практической жизни людей, место нуля в литературном и народном творчестве. Без нуля не было бы современной математики, не было бы таких достижений человеческого разума, как вычислительные машины и космические корабли.
Теперь я смогу рассказать историю появления нуля одноклассникам, показать значимость открытия этой цифры.


















