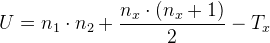Что значит непараметрический критерий

Как правило, любой из параметрических критериев имеет аналог в непараметрической статистике.

Непараметрические критерии представлены следующими основными группами:

Источник

Непараметрические критерии

Общий обзор

Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.

Непараметрические методы позволяют обрабатывать данные «низкого качества» из выборок малого объема с переменными, про распределение которых мало что или вообще ничего не известно.

По существу, для каждого параметрического критерия имеется, по крайней мере, один непараметрический аналог. Эти критерии можно отнести к одной из следующих групп:

критерии различия между независимыми выборками

критерии различия между зависимыми выборками

критерии зависимости между переменными

Различия между независимыми выборками

Две независимые выборки: U-критерий Манна-Уитни и др.

Обычно, когда имеются две выборки (например, мужчины и женщины), которые вы хотите сравнить относительно среднего значения некоторой изучаемой переменной, вы используете t-критерий для независимых выборок.

Непараметрическими альтернативами параметрического критерия для двух независимых групп являются:

Рассмотрим U критерий Манна-Уитни подробнее:

Критерий Манна-Уитни проверяет гипотезу о статистической однородности двух выборок.

Обозначим закон распределения первой выборки X через F:

а второй выборки Y через G:

Законы F и G должны быть непрерывны.

Таким образом нулевая гипотеза записывается в виде

Если по крайней мере одна из групп имеет размер выборки более 15, то можно показать, что:

,

где ,

Несколько независимых групп: критерий Краскела-Уоллиса и др.

Если вы имеете несколько групп, то можете использовать Дисперсионный анализ (ANOVA).

Его непараметрическими аналогами являются:

Рассмотрим критерий Краскела-Уоллиса подробнее:

Критерий Краскела-Уоллиса является расширением критерия Манна-Уитни и предназначен для сравнения распределений в k выборках.

H₁: Распределения каждой из k выборок различны

Критерий Краскела-Уоллиса используется, когда невозможно сказать что-либо определенное об альтернативах , т.к. он свободен от распределения.

Число элементов в каждой i-й выборке ( i=1. k ) равно n_i

Как было показано выше, Заменим наблюдения их рангами , упорядочивая всю совокупность в порядке возрастания.

Затем для каждой выборки необходимо вычислить суммарный и средний ранги:

Если между выборками нет систематических различий, то средние ранги не должны значительно отличаться от среднего, рассчитанного по всей совокупности

Значение последнего .

Здесь — общее число наблюдений.

Вычислим величины дисперсий для каждой выборки

Эти значения при в совокупности должны быть небольшими. Составляя общую характеристику, разумно учесть различия в числе наблюдений для разных выборок и взять в качестве меры отступления от чистой случайности величину

Эта величина называется статистикой Краскела-Уоллеса.

Множитель присутствует в качестве нормировочного для обеспечения сходимости распределения H и с числом степеней свободы .

Согласно стандартному алгоритму проверки гипотез, отвергается на уровне значимости α, если |H| > _кр

Различия между зависимыми выборками

Две зависимые выборки: критерий Вилкоксона и др.

Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке (например, математические успехи студентов в начале и в конце семестра), то обычно используется t-критерий для зависимых выборок.

Альтернативными непараметрическими тестами являются:

Рассмотрим подробнее Критерий Вилкоксона.

Итак, мы располагаем двумя зависимыми выборками. Сформулируем гипотезы:

H₀: медиана разницы в популяции равна нулю

H₁: медиана разницы в популяции не равна нулю.

Вычислим разности для каждой пары результатов.

Обозначим за n’ число ненулевых разностей.

Проранжируем положительные и отрицательные разности (кроме нулевых), чтобы наименьшая абсолютная величина (без учета знака) получила первый ранг.

Отдельно вычислим сумму рангов положительных и отрицательных разностей, меньшую из двух сумм без учета знака считают тестовой статистикой W данного критерия.

Согласно стандартному алгоритму проверки гипотез, отвергается на уровне значимости α, если |W|>Wкр

Если число ненулевых разностей n’>20, статистика W приближается к стандартному нормальному распределению z:

,

Несколько зависимых выборок

Если рассматривается более двух переменных, относящихся к одной и той же выборке, то обычно используется Дисперсионный анализ (ANOVA) с повторными измерениями.

Альтернативным непараметрическим методом является

Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики.

Дело в том, что когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью.

Непараметрические тесты имеют меньшую статистическую мощность (менее чувствительны), чем их параметрические конкуренты, и если важно обнаружить даже слабые отклонения, следует особенно внимательно выбирать статистику критерия.

Источник

Параметрические и непараметрические критерии: различия, особенности применения (ограничения).

Соотношение эмпирического и критического значений критерия является основанием для подтверждения или спростовування гипотезы. Например, в случае применения г-критерия. Стьюдента, если г _ем» г _кр, то значение статистики относятся критической области и нулевая гипотезаН₀ отклоняется (принимается альтернативная гипотеза. Нет). Правила принятия статистического решения оговариваются для каждого критерия

Параметрические и непараметрические критерии

Согласно статистических гипотез статистические критерии делятся на параметрические и непараметрические

. Параметрические критерии используются в задачах проверки параметрических гипотез и включают в свой расчет показатели распределения, например, средние, дисперсии и т.д.. Это такие известные классические критерии, как г-критерий, г-к критерий. Стьюдента, ^-критерий. Фишера и др.. . Непараметрические критерии проверки гипотез основаны на операциях с другими данными, в частности, частотами, рангами и т.п.. Это. А-критерий. Колмогорова-Смирнова, [/-критерий. Вилкок-сона-Манна-Уитни и многие другие

Параметрические критерии позволяют прямо оценить уровень основных параметров генеральных совокупностей, разности средних и различия в дисперсиях. Критерии способны выявить тенденции изменения признака при переходе от условия к ум языка, оценить взаимодействие двух и более факторов в воздействии на изменения признака. . Параметрические критерии считаются несколько более мощными, чем не-параметрические, при условии, что признак измеренная с интервальной шкале и нормально распределенная. Однако с интервальной шкале могут возникнуть определенные проблемы и, если данные, представлены не в стандартизированных оценках. К тому же проверка распределения»на нормальность»требует достаточно сложных расчетов, результат которых заранее неизвестен. Чаще распределения признаков отличаются от нормального, тогда приходится обращаться к непараметрических критерииних критеріїв.

. Непараметрические критерии лишены вышеперечисленных ограничений. Однако они не позволяют осуществить прямую оценку уровня таких важных параметров, как среднее или дисперсия, с их помощью невозможно оценить взаимодействий действие двух и более условий или факторов, влияющих на изменение признаки. Непараметрические критерии позволяют решить некоторые важные задачи, которые сопровождают исследования в психологии и педагогике: выявление различий в уровне исследуемого признака, оценка сдвига значений исследуемого признака, выявление различий в распределениях ознаак.

Применение критериев для принятия (отклонения) статистических гипотез всегда осуществляются с доверительной вероятностью, иначе говоря, на определенном уровне значимости

Критерии выявления различий в уровне исследуемого признака: критерии Розенбаума, Манна-Уитни. Ограничения в применении

Назначение критерия

Критерий используется для оценки различий между двумя вы­борками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 испытуемых.

Описание критерия

Это очень простой непараметрический критерий, который позво­ляет быстро оценить различия между двумя выборками по какому-либо признаку. Однако если критерий Q не выявляет достоверных различий, это еще не означает, что их действительно нет.

В этом случае стоит применить критерий φ* Фишера. Если же Q-критерий выявляет достоверные различия между выборками с уров­нем значимости р

Источник

Непараметрические критерии

Среди них различают 4 группы критериев:

1. Критерии различий – применяют для оценки различий. Например, между двумя или тремы сегментами. Они показывают, действительно ли различия есть или их нет. К ним относят: Q – критерий Розенбаума, U – критерий Манна-Уитни, Н – критерий Крусколо-Уоллеса.

2. Критерии изменений – применяют для доказательства того, что в результате каких-либо действий произошли изменения, сдвиги в измеряемых показателях. К ним относят: G – критерий знаков, Т – критерий Уилкоксона, χ 2 – критерий Фридмена, L – критерий Пейджа.

3. Критерии согласия распределений – применяются для доказательства гипотез по распределению признака, чаще всего доказывается нормальное распределение признака. К ним относят: χ 2 – критерий Пирсона, λ – критерий Колмогорова-Смирнова.

Используется для оценки различий между 2 выборками по уровню какого-либо признака, количественно измеряемого, причем в каждой выборке должно быть не менее 11 испытуемых.

Применяется для оценки различий между 2 выборками. Количество единиц в выборке должно быть больше или равным 3 или, по крайней мере 2 в первой выборке и ≥ 5 – во второй. То есть этот критерий позволяет выявить различия между малыми выборками. Максимальное число не должно превышать 60 наблюдений. Однако уже при 20 ранжирование проблематично.

Применяется для оценки различий между 3, 4 выборками одновременно по уровнюкакого-либо признака. Он позволяет установить, действительно ли уровень признака изменяется при переходе от 1 группы к другой. Но он не указывает, в какую сторону идут изменения. Ограничения: если рассматриваются 3 выборки, то допускается, чтобы в одной было 3 элемента, а в двух других – по 2, но в этом случае значимость критерия находится на самом низком уровне. Для того, чтобы повысить значимость, необходимо, чтобы в каждой выборке было не менее 3 элементов, или хотя бы в одной из них было 4 элемента, а в двух других – по 2.

Предназначен для установления общего направления сдвига исследуемого признака. Он позволяет установить, в какую сторону в выборке изменится значение признака при переходе от первого измерения ко второму (например, до рекламной кампании и после), изменятся показатели в сторону улучшения или ухудшения (ослабления). Количество наблюдений в обоих замерах должно быть не менее 5, но и не более 300.

Применяется для сопоставления показателей, измеренных в 3 или более условиях на одной и той же выборке. Позволяет установить, что показатель от условия к условию изменялся, но не позволяет понять направления изменений. Ограничения: нижний порог – не менее 2 испытуемых, причем каждый из них должен пройти не менее 3 замеров. Верхнего порога нет.

Применяется для сопоставления показателей, измеренных в 3 и более условиях на одной и той же выборке. Позволяет выявить тенденции в изменении величин признака при переходе от одного условия к другому. Его можно рассматривать как продолжение теста Фридмена, то есть он не только констатирует наличие различий, но и указывает направление изменений. Нижний порог – не менее 2 испытуемых и 3 замеров, а верхний – 12 испытуемых и 6 замеров.

Применяется в двух случаях:

1) Для сопоставления эмпирического (фактического) распределения признака с теоретическим (проверка распределения на нормальность)

2) Для сопоставления 2, 3 и более эмпирических распределений между собой. Применяется при объеме выборки – более 30.

Применяется для сопоставления двух распределений – эмпирического с эмпирическим, либо эмпирического с теоретическим. Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения. Критерий требует большой выборки. Если сравниваются 2 эмпирические выборки, то – более 50, а если эмпирическая с теоретической – не менее 5.

Угловое преобразование Фишера

Применяется для сравнения двух выборок по частоте встречаемости интересующего исследователя признака (частота посещения магазина). Критерий оценивает достоверность оценок двух выборок, в которых зарегистрированы интересующие нас группы.

Предназначен для сопоставления частоты встречаемости какого-либо признака с теоретической или заданной частотой. Применяется, когда обследована 1 выборка, объем которой не превышает 300 наблюдений. Критерий позволяет оценить, насколько эмпирическая частота интересующего нас признака больше теоретической (среднестатистической или заданной) частоты.

Источник

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

U-КРИТЕРИЙ МАННА-УИТНИ

– непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.

1. История разработки U-критерия

Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном.
В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.

Хенри Манн

2. Для чего используется U-критерий Манна-Уитни?

U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.

3. В каких случаях можно использовать U-критерий Манна-Уитни?

U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.

U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.

Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.

Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.

4. Как рассчитать U-критерий Манна-Уитни?

Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.

Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.

В составленном едином ранжированном ряду общее количество рангов получится равным:

Наконец, находим значение U-критерия Манна-Уитни по формуле:

5. Как интерпретировать значение U-критерия Манна-Уитни?

Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок:

Источник