Что значит множество ограничено сверху

Ограниченные множества

Пусть непустое множество действительных чисел.

У ограниченного сверху множества существует сколь угодно много верхних границ. Действительно, если верхняя граница множества то для любого положительного число также является верхней границей Аналогично, у ограниченного снизу множества существует сколь угодно много нижних границ.

С геометрической точки зрения ограниченность сверху множества означает наличие на числовой прямой такой точки что все точки множества расположены не правее Аналогично, ограниченность снизу множества означает наличие на числовой прямой такой точки что все точки множества расположены не левее, чем

С геометрической точки зрения ограниченность означает, что все точки множества содержатся в некотором отрезке числовой прямой.

Определение. Элемент называется наибольшим элементом множества если для любого справедливо неравенство Элемент называется наименьшим элементом множества если для любого справедливо неравенство

Очевидно, что если во множестве существует наибольший элемент, то это множество ограничено сверху, а если в существует наименьший элемент, то это множество ограничено снизу. Однако не каждое ограниченное сверху (снизу) множество имеет наибольший (наименьший) элемент. Например, множество ограничено сверху (например, числом однако в нем нет наибольшего элемента. Действительно, для любого число x» title=»z=\frac < x+1 > < 2 >> x» /> также принадлежит Аналогично можно показать, что ограничено снизу, но не имеет наименьшего элемента.

Пусть – ограниченное сверху множество. Через обозначим совокупность всех верхних границ множества Множество непусто и, как мы уже видели, неограничено сверху. Очевидно, однако, что ограничено снизу (например, любой элемент множества является нижней границей множества

Поставим следующий вопрос: существует ли во множестве наименьший элемент?

Это определение равносильно следующему.

Определение. Число называется верхней гранью множества если выполнены следующие два условия:

Первое условие этого определения означает, что является верхней границей множества а второе – что наименьшая из всех верхних границ, т. е. что никакое число не является верхней границей множества

Аналогично формулируется определение нижней грани.

Это определение равносильно следующему.

Определение. Число называется нижней гранью множества если выполнены следующие два условия:

Первое условие этого определения означает, что m является нижней границей множества а второе – что наибольшая из всех нижних границ, т. е. что никакое число m» title=»+\varepsilon > m» /> не является нижней границей множества

Из определения верхней и нижней граней множества не следует сам факт их существования. Существование точных границ устанавливает следующая теорема.

Теорема (о существовании верхней грани). Каждое непустое ограниченное сверху множество имеет верхнюю грань. Пусть ограниченное сверху множество, а множество всех его верхних границ. Оба множества непустые, и для любых справедливо неравенство По аксиоме полноты множества действительных чисел, существует такое число что для любых справедливо неравенство Левое неравенство означает, что число является верхней границей множества т. е. а правое неравенство показывает, что наименьший элемент во множестве

Аналогично доказывается следующая

Теорема (о существовании нижней грани). Каждое непустое ограниченное снизу множество имеет нижнюю грань.

Понятие верхней (нижней) грани мы определили для ограниченного сверху (снизу) множества. Но не каждое множество ограничено сверху (снизу). Так, само множество действительных чисел неограничено сверху и снизу. В самом деле, для любого найдется такой, что M» title=»x > M» /> (например, Это означает, что никакое число не является верхней границей множества В случае если множество неограничено сверху, иногда пишут Аналогично, если множество неограничено снизу, то пишут Примером неограниченного снизу множества также может быть множество

Задание 1
Пусть 1. Доказать, что множество не имеет ни наименьшего, ни наибольшего элементов.

Действительно, для любого число x» title=»z=\frac < x+\sqrt < 2 >> < 2 >> x» /> также принадлежит следовательно, не имеет наибольшего элемента. Аналогично можно показать, что не имеет наименьшего элемента.

Действительно, всякие вещественные будут элементами множества и 0,» title=»\forall \varepsilon > 0,» /> по аксиоме полноты множества действительных чисел, существует такой что т. е. какое бы вещественное число из мы не взяли, можно выбрать другое число из так, что оно будет находиться ближе к на числовой прямой.

Аналогично доказывается, что

Задание 2
Пусть непустые ограниченные множества неотрицательных действительных чисел, множество всевозможных чисел где Показать, что ограниченное множество, причём

По теореме о существовании верхней грани, из ограниченности и следует существование и Тогда справедливы неравенства: из которых следует, что т. е. является верхней границей множества Кроме того, поскольку и – множества неотрицательных действительных чисел, т. е. является нижней границей множества Отсюда следует, что множество ограничено.

Поскольку и соответственно являются верхними гранями множеств и справедливы неравенства 0\quad \forall x\in X:< M >_< 1 >-\varepsilon 0\quad \forall x\in X:< M >_< 1 >-\varepsilon 0\quad \forall y\in Y:< M >_< 2 >-\varepsilon 0\quad \forall y\in Y:< M >_< 2 >-\varepsilon из которых следует: 0\quad \forall x\in X\quad \forall y\in Y:» title=»\forall < \varepsilon >_< 1 >,< \varepsilon >_ < 2 >> 0\quad \forall x\in X\quad \forall y\in Y:» /> Обозначим: Получим неравенство 0\quad \forall x\in X\quad \forall y\in Y:< M >_< 1 >< M >_< 2 >—< \varepsilon >_ < 3 >0\quad \forall x\in X\quad \forall y\in Y:< M >_< 1 >< M >_< 2 >—< \varepsilon >_ < 3 >. Из него и из неравенства следует, что что и требовалось доказать.

Забегая вперёд, при рассмотрении следующего задания используем материал урока «Определение и элементарные свойства».

Источник

Точечные множества

Множества, элементами которых являются точки, называются точечными множествами. Таким образом, можно говорить о точечных множествах на прямой, на плоскости, в каком-либо пространстве. Ради простоты мы ограничимся рассмотрением точечных множеств на прямой.

Между действительными числами и точками на прямой имеется тесная связь: каждому действительному числу можно отнести точку на прямой и обратно. Поэтому, говоря о точечных множествах, мы будем причислять к ним и множества, состоящие из действительных чисел — множества на числовой прямой. Обратно: для того чтобы задать точечное множество на прямой, мы будем обычно задавать координаты всех точек нашего множества.

Точечные множества (и, в частности, точечные множества на прямой) обладают рядом особых свойств, отличающих их от произвольных множеств и выделяющих теорию точечных множеств в самостоятельную математическую дисциплину. Прежде всего имеет смысл говорить о расстоянии между двумя точками. Далее, между точками на прямой можно установить соотношения порядка (левее, правее); в соответствии с этим говорят, что точечное множество на прямой является упорядоченным множеством. Наконец, как уже отмечалось выше, для прямой справедлив принцип Кантора; это свойство прямой принято характеризовать как полноту прямой.

Введем обозначения для простейших множеств на прямой.

Начнем с рассмотрения различных возможностей расположения множества в целом на прямой.

Ограниченные и неограниченные множества

Нетрудно видеть, что если — фиксированная точка на прямой, то множество будет ограничено в том и только в том случае., если расстояния от точки до любой точки не превосходят некоторого положительного числа.

Множества, ограниченные сверху и снизу

Ясно, что данное выше определение ограниченного множества эквивалентно следующему: множество точек на прямой называется ограниченным, если оно ограничено сверху и снизу. Несмотря на то, что эти два определения очень похожи друг на друга, между ними имеется существенное различие: первое основано на том, что между точками на прямой определено расстояние, а второе, что эти точки; образуют упорядоченное множество.

Верхняя и нижняя грань множества

Расположение точечного множества вблизи какой-либо точки на прямой

Укажем несколько примеров, поясняющих все эти понятия.

Пример 1. Пусть множество состоит из точек с координатами

Пример 4. Пусть множество состоит из всех точек с целыми координатами на прямой. Каждая точка является его изолированной точкой; множество не имеет предельных точек.

Теорема Больцано-Вейерштрасса

Всякое ограниченное бесконечное множество точек на прямой имеет хотя бы, одну предельную точку.

Источник

Точные грани числовых множеств

Верхняя и нижняя грани числовых множеств.

Множество X вещественных чисел (X ⊂ \(\mathbb\)) называется ограниченным сверху, если существует вещественное число C такое, что все элементы множества X не превосходят C, то есть
$$
\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \leq \ C.\label
$$

Всякое вещественное число C, обладающее свойством \eqref, называется верхней гранью числового множества X.

Аналогично, множество X ⊂ \(\mathbb\) называется ограниченным снизу, если
$$
\exists C’\in\mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geq \ C’.\label
$$

Всякое вещественное число С ‘ , удовлетворяющее условию \eqref, называют нижней гранью числового множества X.

Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb\ \exists C\in\mathbb: \ \forall x\in X \ \rightarrow \ C’ \ \leq \ x \ \leq \ C\right\>\).

Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb\)>.

По условию \(B=\left\<\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geqslant \ C\right\>\). Поэтому
$$
\rceil B=\left\<\forall C \ \in \ \mathbb: \ \exists x_C \ \in \ X \ \rightarrow \ x_C Определение 1.

Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:

Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.

Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.

Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:

Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.

Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:

Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref. Пусть C=c₀,c₁c₂…c_n…; тогда c₀ — неотрицательное целое число, причем C x’.\label$$

Возьмем произвольное число x ∈ X и пусть x = a₀,<a_n>. Чтобы проверить выполнение условия \eqref, рассмотрим три произвольных случая:

$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$\exists m: \ x\in X_, \ x\not\in X_\label$$

Из \eqref следует, что \(a_0 удовлетворяет произвольный элемент \(\widetilde x\in X_m\), так как

Из неравенства \eqref следует, что sup X есть нижняя грань множества Y. Точная нижняя грань множества Y, то есть число inf Y, есть наибольшая из всех нижних граней множества Y. Значит, sup X ≤ inf Y.

Источник

Грани числовых множеств

Грани числовых множеств

Говорят, что множество ограничено сверху (снизу), если существует такое число , что для любого . Число в этом случае называется верхней (нижней) гранью множества X.

Множество, ограниченное и сверху, и снизу, называется ограниченным, т. е. существуют два числа , такие, что , . Эти неравенства показывают, что множество X ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество X ограничено тогда и только тогда, когда существует положительное число С, такое, что

Множество, не ограниченное сверху или снизу, называется неограниченным.

Если число является верхней гранью множества X, то и любое число больше тоже является верхней гранью, и, если число -нижняя грань множества X, то всякое число, меньше будет нижней гранью X.

Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (нижней) гранью множества и обозначается символом («супремум X») (, «инфимум X»).

Точные верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если множество X не ограничено сверху (снизу), то иногда используют обозначение .

Теорема 1*. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.

Эта лекция взята со страницы лекций по предмету математический анализ:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

5.01 О границах числовых множеств

Множество, элементами которого являются вещественные числа, будем называть числовым. Если множество состоит из конечного числа элементов, то его называют конечным, в противном случае – бесконечным.

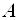
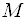
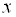
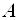
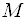
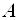
Определение. Числовое множество называется ограниченным сверху, если существует такое вещественное число , что для любого элемента из множества выполняется неравенство . Число называется верхней границей .

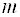
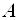
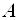
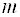
Определение. Если существует такое число , что все элементы множества удовлетворяют неравенству , то множество называется ограниченным снизу, а число – его нижней границей.

Определение. Числовое множество 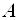называется ограниченным, если оно ограничено сверху и снизу, т. е. если для всех выполняется неравенство .

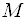
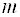
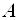
Если – верхняя, а – нижняя границы множества , то числа и тоже будут соответственно верхней и нижней границами этого множества. Следовательно, всякое ограниченное множество имеет бесконечно много верхних и нижних границ.

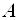
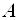
Определение. Наименьшая из всех верхних границ множества называется точной верхней границей этого множества (обозначается ). Наибольшая из всех нижних границ называется точной нижней границей этого множества (обозначается ).

Точная верхняя и точная нижняя границы могут как принадлежать данному множеству, так и не принадлежать ему.

Если 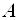не ограничено сверху, то пишут , если снизу, то .

На вопрос о том, всегда ли у ограниченного множества существуют точные границы, отвечает следующая теорема.

Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю границу, а всякое непустое ограниченное снизу множество имеет точную нижнюю границу.

Пример 1. Даны множества , и . Указать их точные границы.

Решение. – бесконечное, ограниченное снизу множество. Числа – его нижние границы, а . Сверху это множество не ограничено, т. е. . Множество – бесконечное ограниченное множество, т. е. оно ограничено и сверху, и снизу, его точные границы: , , – бесконечное множество, не ограниченное как сверху, так и снизу.

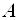
Любое конечное множество ограничено, так как среди его элементов всегда найдутся наибольшее и наименьшее числа, которые и будут точными границами. Обратное утверждение неверно, т. е. из ограниченности множества не следует его конечность, как это видно на примере множества .

Пример 2. Числовое множество состоит из всех чисел, для которых . Какие числа будут его границами?

Решение. Неравенство равносильно двойному неравенству , откуда видно, что число 3 и всякое большее число будет верхней границей, а число –3 и всякое меньшее число – его нижней границей. , .

Пример 3. Числовое множество состоит из чисел, удовлетворяющих условию . Укажите наименьшее число , удовлетворяющее неравенству для всех из данного множества. Какими границами для этого множества будут числа и ?

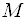
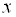
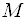
Решение. Так как равносильно неравенству , то за нужно взять такое положительное число, чтобы неравенства: и выполнялись одновременно. Это, очевидно, будет при , равном наибольшей из абсолютных величин чисел и , то есть при , при этом , a – верхняя (не точная) граница , точной верхней границей является .

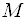
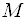
Вопросы для самопроверки.

1. Приведите примеры ограниченных бесконечных множеств. Существуют ли конечные неограниченные множества?

2. Приведите примеры множеств, которым принадлежат их точные границы и множеств, которым не принадлежат их точные границы.

3. Приведите пример множества, которому принадлежит его точная нижняя граница, а точная верхняя не принадлежит.

Источник