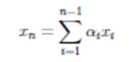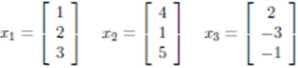Что значит линейная зависимость

Линейная зависимость и независимость, свойства, исследование системы векторов на линейную зависимость, примеры и решения.

Понятия линейной зависимости и независимости системы векторов является очень важными при изучении алгебры векторов, так как на них базируются понятия размерности и базиса пространства. В этой статье мы дадим определения, рассмотрим свойства линейной зависимости и независимости, получим алгоритм исследования системы векторов на линейную зависимость и подробно разберем решения примеров.

Навигация по странице.

Определение линейной зависимости и линейной независимости системы векторов.

Так мы подошли к определению линейной зависимости системы векторов .

Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.

Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.

Свойства линейной зависимости и независимости.

На основании данных определений, сформулируем и докажем свойства линейной зависимости и линейной независимости системы векторов.

Если к линейно зависимой системе векторов добавить несколько векторов, то полученная система будет линейно зависимой.

Так как система векторов линейно зависима, то равенство возможно при наличии хотя бы одного ненулевого числа из чисел . Пусть .

Добавим к исходной системе векторов еще s векторов , при этом получим систему . Так как и , то линейная комбинация векторов этой системы вида

представляет собой нулевой вектор, а . Следовательно, полученная система векторов является линейно зависимой.

Если из линейно независимой системы векторов исключить несколько векторов, то полученная система будет линейно независимой.

Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно.

Если в системе векторов есть хотя бы один нулевой вектор, то такая система линейно зависимая.

Пусть вектор в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство возможно только тогда, когда . Однако, если взять любое , отличное от нуля, то равенство все равно будет справедливо, так как . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.

Если система векторов линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов линейно независима, то ни один из векторов не выражается через остальные.

Сначала докажем первое утверждение.

Пусть система векторов линейно зависима, тогда существует хотя бы одно отличное от нуля число и при этом верно равенство . Это равенство можно разрешить относительно , так как , при этом имеем

Следовательно, вектор линейно выражается через остальные векторы системы , что и требовалось доказать.

Теперь докажем второе утверждение.

Так как система векторов линейно независима, то равенство возможно лишь при .

Предположим, что какой-нибудь вектор системы выражается линейно через остальные. Пусть этим вектором является , тогда . Это равенство можно переписать как , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.

Из двух последних свойств следует важное утверждение:
если система векторов содержит векторы и , где – произвольное число, то она линейно зависима.

Исследование системы векторов на линейную зависимость.

Поставим задачу: нам требуется установить линейную зависимость или линейную независимость системы векторов .

Логичный вопрос: «как ее решать?»

Кое-что полезное с практической точки зрения можно вынести из рассмотренных выше определений и свойств линейной зависимости и независимости системы векторов. Эти определения и свойства позволяют нам установить линейную зависимость системы векторов в следующих случаях:

Как же быть в остальных случаях, которых большинство?

Напомним формулировку теоремы о ранге матрицы, которую мы приводили в статье ранг матрицы: определение, методы нахождения.

А теперь поясним связь теоремы о ранге матрицы с исследованием системы векторов на линейную зависимость.

Что будет означать линейная независимость системы векторов ?

Что же будет означать линейная зависимость системы векторов ?

Все очень просто: хотя бы одна строка матрицы A будет линейно выражаться через остальные, следовательно, линейная зависимость системы векторов будет равносильна условию Rank(A)

Итак, задача исследования системы векторов на линейную зависимость сводится к задаче нахождения ранга матрицы, составленной из векторов этой системы.

Следует заметить, что при p>n система векторов будет линейно зависимой.

Замечание: при составлении матрицы А векторы системы можно брать не в качестве строк, а в качестве столбцов.

Алгоритм исследования системы векторов на линейную зависимость.

Разберем алгоритм на примерах.

Примеры исследования системы векторов на линейную зависимость.

Дана система векторов . Исследуйте ее на линейную зависимость.

Так как вектор c нулевой, то исходная система векторов линейно зависима в силу третьего свойства.

система векторов линейно зависима.

Исследуйте систему векторов на линейную зависимость.

система векторов линейно зависима.

Является ли система векторов линейно зависимой?

Является ли система векторов линейно независимой?

Докажите, что система векторов

линейно независима.

Составим матрицу, строками которой будут векторы данной системы:

Покажем, что ранг этой матрицы равен количеству векторов исходной системы, то есть, четырем.

Переходим к поиску окаймляющего минора третьего порядка:

Осталось найти минор четвертого порядка, отличный от нуля. Вычислим определитель

Прибавим к первому столбцу третий, далее разложим определитель по элементам первого столбца:

Таким образом, ранг матрицы А равен четырем что доказывает линейную независимость исходной системы векторов.

Мы ознакомились с понятиями и свойствами линейной зависимости и линейной независимости системы векторов, получили метод исследования системы векторов на линейную зависимость, преобразовали его в алгоритм, и подробно разобрали решения характерных примеров.

Источник

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник