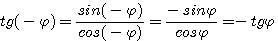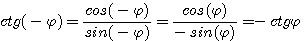Что значит косинус четная функция
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №2 Чётность и нечётность тригонометрических функций. Периодичность.
Перечень вопросов, рассматриваемых в теме
Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x).
Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.
Область. определения функции (D) — множество R всех действительных чисел
Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.
Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная
Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.
Область определения функции (D) — множество R всех действительных чисел.
Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.
Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная


Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Выясним, является ли функция
чётной или нечётной?
Пример 2. Доказать, что число 2π является наименьшим положительным периодом функции y=cos x
Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π
Что значит косинус четная функция
ЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
Четность тригонометрических функций.
Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки).
Поэтому конечные стороны OA 1 и ОА 2 этих углов симметричны относительно оси абсцисс.
Следовательно, синус является нечетной, а косинус — четной функцией угла.
Поэтому тангенс и котангенс являются нечетными функциями угла.
Выяснить, какие из данных функций являются четными и какие нечетными:
1) у = sin (—х); 4) у = sin x cos х; 7) у = sin 2 x;
2) у = cos (—х); 5) у = sec x; 8) у = cos 2 x;
3) у = tg (2х); 6) у = cosec x; 9) у = sin x + tg x.
Периодичность функций sin φ и cos φ
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.
Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.
Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.
Пусть f(х) есть некоторое выражение, зависящее от переменной величины х.
(Например, f(х) = x 2 , f(х) = sin x и т. д.)
Определяет у как функцию аргумента х.
Если при любых допустимых значениях аргумента х
где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.
Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.
При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.
Таким образом, cos φ = cos (φ + 360°n),
sin φ = sin (φ + 360°n), (1)
где n — любое целое число (положительное, отрицательное или нуль).
Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.
Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ
В частности, при φ = 0 получаем: sinТ = sin 0° = 0.
Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы
Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.
1. Доказать следующие соотношения:
а) sin 740° = sin 20°; в) cos 54° = cos (—1026°);
б) sin (—1000°) = sin 80°; г) cos (—1750°) = cos 50°.
2. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 360°:
a) sin 820°; б) cos (—7363°); в) sin (—600°).
3. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 180°:
a) cos 729°; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).
4. Доказать, что угол в 540° является одним из периодов функции у = cos2х.
5. Доказать, что угол и 360° является одним из периодов функции у = tgx.
6. Докажите, что любой период Т функции у = cos х является корнем уравнения
Верно ли обратное утверждение?
Периодичность функций tg φ и ctg φ
Следовательно, при любом φ
Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?
Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть
В частности, при φ = 0° получаем:
Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом (то есть наименьшим положительным периодом) функции tg φ является угол в 180°.
Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.
1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (—185°); в) ctg 300°; г) ctg (—210°).
2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90°:
3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.
4. Доказать, что любой период Т функции у = ctg х является корнем уравнения
Верно ли обратное утверждение?
О периодических функциях.
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.
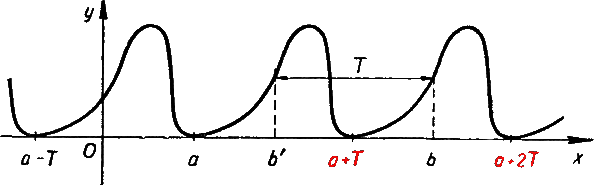
Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.
Покажем, как можно определить значения этой функции в интервале ( а + Т, а + 2 T ).
Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.
В силу периодичности функции f(x)
Таким образом, по заданным значениям функции f
Итак, задание периодической с периодом Т функции f(x) на любом интервале длины Т дает возможность полностью охарактеризовать ее на всей числовой прямой. Поэтому для исследования функции f(x), периодической с периодом Т, достаточно изучить ее поведение лишь на каком-нибудь интервале длины Т. Например, для исследования функций у = sin φ и у = cos φ достаточно рассмотреть их лишь при 0° <φ <360°. Для исследования функции у = tg φ можно было бы ограничиться интервалом 0° <φ <180°. Но при φ = 90° tg φ не определен. Поэтому в данном случае целесообразнее выбрать какой-нибудь другой интервал, в каждой точке которою функция у = tg φ была бы определена. Мы отдадим предпочтение интервалу —90° < φ < 90°. Однако в принципе можно было бы выбрать, конечно, и интервал 0° <φ <180°. Для изучения функции сtg φ целесообразно выбрать интервал 0° < φ < 180°.
2. Может ли периодическая с периодом Т функция f(x) удовлетворить условию
Если может, то в каком случае? Ответ пояснить примерами.
14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
Промежутки возрастания и убывания
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке
то при увеличении аргумента x (x 2 > x 1 ) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
делаем вывод, что она такж е возрастает на каждом из промежутков
Если x ∈ 
окружности уменьшается (то есть sin x 2 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
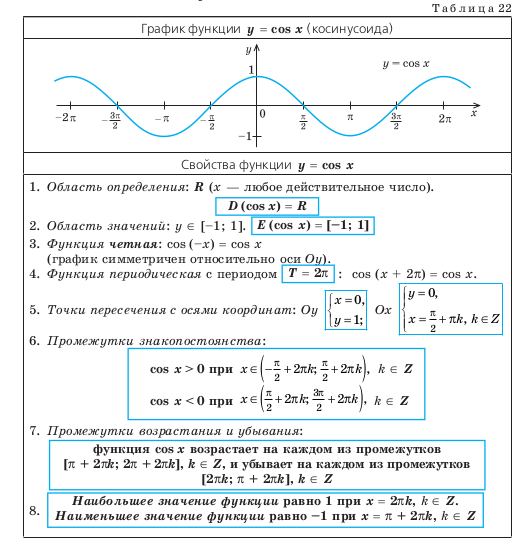
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это
зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x. Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки