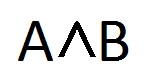Что значит конъюнкция в информатике
Логические операции. ➞ Что такое конъюнкция, дизъюнкция, импликация
Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.
Основные положения
Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.
Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).
Примером таким высказываний будут являться:
Логические высказывания делятся на два типа — простые и сложные.
В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.
Булево выражение – это символическое (знаковое) описание высказывания.
Операции
Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.
Конъюнкция
Конъюнкция (булево умножение) — функция, по своему смыслу приближенная к союзу «И». При выполнении конъюнкции результат истинен (равен 1) тогда и только тогда, когда истинны ВСЕ переменные. Если хотя бы одно из высказываний ложно, то ложно и всё выражение (равно 0).
Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:
Дизъюнкция
Дизъюнкцией называется функция булева сложения. По смыслу дизъюнкция приближена к союзу «ИЛИ». В результате выполнения данной функции результирующие выражение является истинным, когда хотя бы одно из высказываний в этом выражении тоже истинно.
Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.
Инверсия
Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.
Импликация
Также называется булевым следованием. В русском языке данной функции соответствует оборот «Если …, то …». Например, если на улице гремит гром, то стоит пасмурная погода.
Эквивалентность
Булева тождественность или равенство. На простом языке будет обозначено как «… эквивалентно (равно) …». Результат будет истинным тогда, когда все значения в выражении будут иметь одинаковую истинность.
Обозначается с помощью трех черточек или ⟺.
Порядок выполнения операций
Логические операции выполняются в следующем порядке:
Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.
Пример
Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:
Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:
Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.
Таблица истинности для всех отрезков:
Ответ: A = [3,11].
Видео
Заключение
Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.
Конъюнкция
Логическая операция конъюнкция — бинарная операция над высказываниями, результатом которой является истинное высказывание только в случае, когда исходные высказывания истинны.
Другие названия конъюнкции — логическое умножение, логическое И или просто И.
Конъюнкция изучается в информатике при рассмотрении раздела алгебра логики.
В естественных языках конъюнкцию заменяют союзом «и».
В языках программирования для конъюнкции используют обозначение ‘ and ‘ или знак амперсанд ‘ & ‘ (либо ‘ && ‘) (например, x>0 and x или a>=10 & a ).
Как набрать знак конъюнкции на клавиатуре
Таблица истинности для конъюнкции
Истинность конъюнкции определяется ее таблицей истинности.
| A | B | A /\ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Конъюнкция и круги Эйлера
Результатом конъюнкции является область пересечения высказываний.
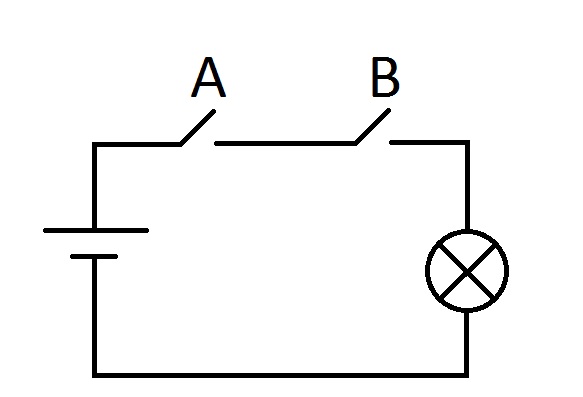
Электрический аналог конъюнкции
Представим, что выключатели A и B — это высказывания, причем 0 — выключатель разомкнут, 1 — выключатель замкнут. Лампа символизирует конъюнкцию. Когда она не горит — 0, горящая лампа — 1. Тогда становится очевидным, что лампа будет гореть только когда оба выключателя будут замкнуты, что полностью соотносится с таблицей истинности для конъюнкции.
Урок на тему «Логические операции. Конъюнкция»
В предыдущем уроке мы рассмотрели логическую операцию отрицание. Сегодня поговорим о конъюнкции. Конъюнкцию также называют «логическое умножение» или «логическое И«, а часто просто «И«.
В естественном языке конъюнкцию заменяют союзом И.
Конъюнкция — бинарная операция, т. е. для нее необходимо два операнда.
Для обозначения конъюнкции применяют различные символы. Это может быть знак &, AND. Но чаще всего для обозначения конъюнкции используют символ
Рассмотрим пример. Пусть есть два высказывания: A = «Москва — столица России» и B = «Сегодня солнечно«. Тогда конъюнкция этих высказываний будет выглядеть так «Москва — столица России И сегодня солнечно«, а обозначаться так:
Так как на клавиатуре нет символа конъюнкции, его можно набрать из слэша ( / ) и бэкслэша ( \ ) — получится /\ — похоже на обозначение конъюнкции.
Таблица истинности для конъюнкции выглядит так:
| A | B | A /\ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Запомнить довольно просто — конъюнкция истинна только в одном случае — когда оба исходных высказывания истинны. А еще проще запомнить таблицу истинности для конъюнкции, если представить ее электрический аналог — два последовательно включенных выключателя:
Электрический аналог конъюнкции
И теперь сразу понятно, что лампочка будет гореть только тогда, когда оба выключателя включены — цепь замкнута. Все также как и у конъюнкции.
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Логика
НЕКОТОРЫЕ
СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Обозначения
1.1. Обозначения для логических связок (операций):
a) отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
b) конъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В);
c) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/
(например, А \/ В);
d) следование (импликация) обозначается → (например, А → В);
e) тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).
1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А /\ В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А \/ В \/ С \/ D означает то же, что и
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
2. Свойства
Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.
2.1. Общие свойства
2.2.Дизъюнкция
2.3. Конъюнкция
2.4. Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
2.5. Импликация
Что значит конъюнкция в информатике
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность: