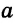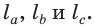Что значит искомый треугольник

Задачи на экстремум в планиметрии

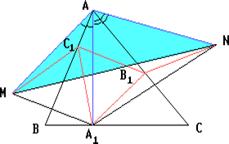
Отсюда следует, что искомый треугольник — это треугольник с вершинами в основаниях высот данного, т.е. ортотреугольник данного треугольника. Действительно, пусть AA», BB» и CC» — высоты треугольника ABC, а точки A1, B1 и C1 расположены на сторонах соответственно BC, AC и AB. Если треугольник A1B1C1 не совпадает с треугольником A»B»C», то по ранее доказанному

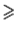
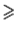
P A1B1C1 PA»B1C1 PA»PQ,

где P и Q — точки пересечения прямой MN со сторонами соответственно AB и AC треугольника ABC. При этом хотя бы один из знаков неравенства — строгий. Значит, искомый треугольник минимального периметра — это треугольник A»PQ. Если бы точка P не совпадала с точкой C», то, повторив предыдущие рассуждения, построили бы треугольник, площадь которого меньше площади треугольника A»PQ, что невозможно. Аналогично для точки Q. Таким образом, точка P совпадает с C», а точка Q — с точкой B».

1. Изложенное решение основано на доказательстве Фейера (L.Fejer). Это, а также другие изящные доказательства данного утверждения (Г.А.Шварц, Л.Шрутка, Бюкнер) см. в книге Г.Радемахера и О.Теплица «Числа и фигуры» (М.,1962, с.36-46).

2. Другой способ доказательства того, что точки P и Q пересечения прямой MN со сторонами соответственно AB и AC также будут основаниями высот треугольника ABC.

Поскольку AM = AA» = AN, то точки M, A» и N лежат на окружности с центром A и радиусом AA». Тогда

A»NP = A»AP

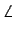
(вписанный угол равен половине соответствующего центрального). Поэтому из точек A и N отрезок A»P виден под одним и тем же углом. Значит, точки A, P, A», N лежат на одной окружности.

С другой стороны, треугольники AA»C и ANC симметричны относительно прямой AC, поэтому они равны. Значит, из точек A» и N отрезок AC виден под прямым углом, поэтому эти точки лежат на окружности с диаметром AC. Поскольку через три точки, не лежащие на одной прямой, проходит ровно одна окружность, то все пять точек A, P, A», C и N лежат на окружности с диаметром AC. Тогда из точки P диаметр AC виден под прямым углом, т.е. CP — высота треугольника ABC. Аналогично докажем, что BQ — также высота треугольника ABC.

В этой курсовой работе я изучила некоторые теоремы, позволяющие решать задачи на экстремумы, проиллюстрировала их применение.

В заключение этой работы, на мой взгляд, следует провести однозначную черту под бесспорным фактом целесообразности и полезности применения ряда задач элементарной геометрии на построение некоторых фигур таким образом, чтобы один из параметров получил наибольшее или наименьшее значение. Во многих случаях решение можно получить без применения методов математического анализа.

1. С.И. Зетель, «Задачи на максимум и минимум», Москва

2. С.А. Теляковский, «Алгебра», Москва, 2001г.

3. Ю.Н. Макарычев, «Математика», Москва, 1988г.

4. Г.С.М. Коксетер, С.П. Грейтцер, «Новые встречи с геометрией», 1978г.

Источник

Существующие треугольники

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

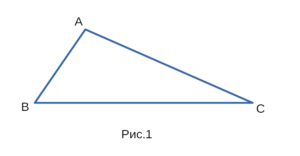
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

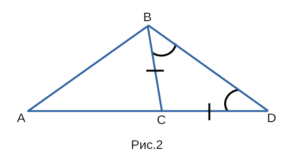
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

Источник

Признаки равенства треугольников

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Задачи на построение по геометрии с примерами решения

Содержание:

Ранее мы выполняли построения на плоскости при помощи линейки с делениями, чертежного треугольника, транспортира и циркуля.

Математиков всегда интересовали построения геометрических фигур, которые можно выполнить только при помощи циркуля и линейки. В геометрии специально выделяют задачи на построение, которые могут быть решены с помощью этих двух инструментов.

Например, при помощи циркуля и линейки можно построить треугольник, стороны которого равны трем данным отрезкам. Или построить угол, равный данному углу.

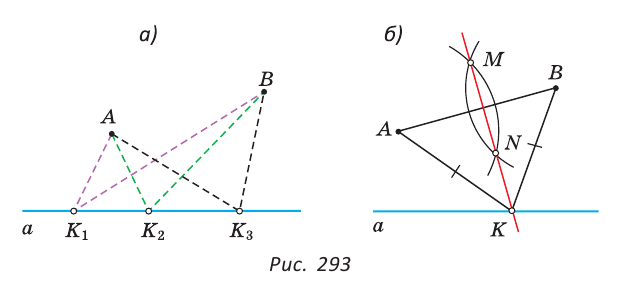
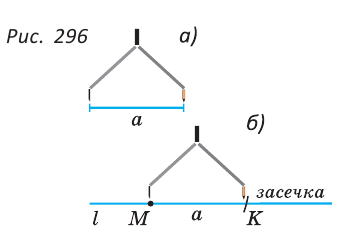
Рассмотрим одну из таких задач на построение. На прямой

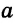
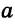
Найти точку — это значит построить ее при помощи циркуля и линейки. Если перемещать некоторую точку по прямой (положения К₁ К₂, К₃), то расстояния от этой точки до точек А и В будут меняться. Когда эти расстояния станут равными, точка на прямой будет равноудалена от концов отрезка АВ. Значит, она будет лежать на серединном перпендикуляре к отрезку АВ. Это и есть идея построения: нужно построить серединный перпендикуляр к отрезку АВ и найти точку его пересечения с прямой .

Чтобы построить серединный перпендикуляр, нужно построить две пересекающиеся окружности равных радиусов с центрами в точках А к В (рис. 293, б). Затем провести прямую MN через точки пересечения этих окружностей (ниже мы обоснуем это построение). В пересечении серединного перпендикуляра MN к отрезку АВ и прямой 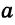получим искомую точку К.

Рассмотренная задача может иметь и практический смысл. Допустим, есть два населенных пункта и шоссе рядом с ними. На шоссе нужно найти место для остановки, чтобы путь для жителей обоих населенных пунктов до остановки был одинаковым. Все построения будут сделаны на карте населенного пункта.

При решении задач на построение линейка считается односторонней и без делений. При помощи такой линейки нельзя построить две параллельные прямые, проведя линии по краям линейки, нельзя измерять и откладывать отрезки, нельзя строить перпендикуляры, используя прямоугольную форму линейки. Рассмотрим, какие операции можно выполнять линейкой, а какие циркулем.

Операции с линейкой

При помощи линейки можно провести (построить):

а) произвольную прямую;

б) прямую, проходящую через две точки (рис. 294).

Операции с циркулем

При помощи циркуля можно:

а) построить произвольную окружность и окружность (дугу окружности) с данным центром и радиусом, равным данному отрезку (рис. 295);

б) отложить отрезок, равный данному отрезку, на некоторой прямой.

Откладывание отрезка

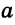
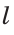
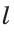
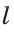
Для откладывания отрезка, равного данному отрезку (рис. 296, а) на прямой (рис. 296, б), следует: 1) отметить на прямой точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой ).

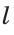
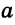
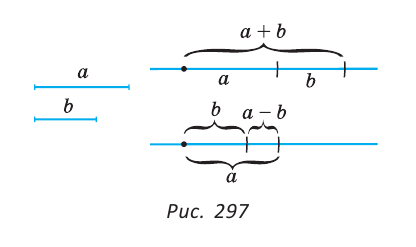
В пересечении дуги и прямой получим точку К и отрезок МК, равный .

Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.

В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.

Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.

В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».

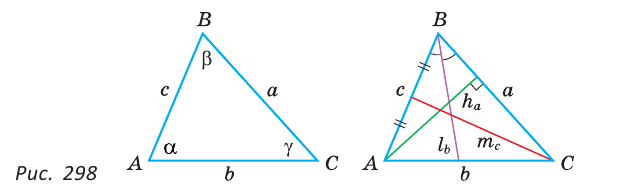
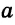
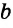
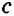
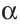
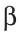
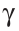
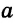
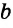
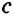
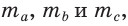
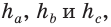
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать , и , а сами эти углы — , и (рис. 298). Медианы, проведенные к сторонам , и , — высоты — биссектрисы —

Построение треугольника по трем сторонам. Построение угла, равного данному

Задача №1

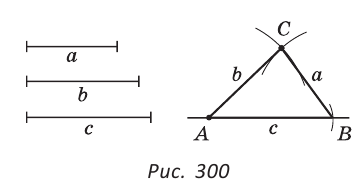
Построить треугольник со сторонами , и .

Решение:

Пусть даны отрезки , и . На произвольной прямой откладываем отрезок АВ = (рис.300).

Строим окружность с центром в точке А радиусом . Строим окружность с центром в точке В радиусом . Находим точку С пересечения этих окружностей. Проведем отрезки АС и ВС.

Треугольник ABC — искомый, так как у него ВС = , АС = , АВ = по построению.

Задача имеет решение, если для данных отрезков , и выполняется неравенство треугольника:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Треугольник и его виды

Из всех многоугольников треугольники имеют наименьшее количество углов и сторон.

Треугольники можно различать по виду их углов.

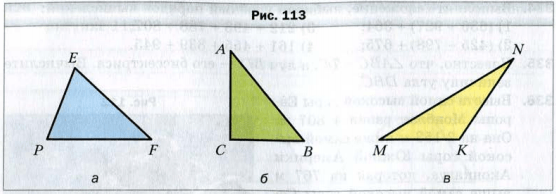
Есди все углы треугольника острые, то его называют остроугольным треугольником (рис. 113, а).

Если один из углов треугольника прямой, то его называют прямоугольным треугольником (рис. 113, б).

Если один из углов треугольника тупой, то его называют тупоугольным треугольником (рис. 113, в).

Говорят, что мы классифицировали треугольники по виду их углов.

Треугольники можно классифицировать не только по виду углов, но и по количеству равных сторон.

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

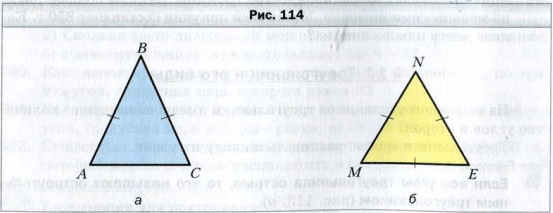
На рисунке 114, а изображен равнобедренный треугольник ABC, у которого AB = BC. На рисунке равные стороны отмечают равным количеством черточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC − основанием равнобедренного треугольника ABC.

Если стороны треугольника равны, то его называют равносторонним треугольником.

Треугольник, изображенный на рисунке 114, б, − равносторонний, у него MN = NE = EM.

Треугольник, у которого три стороны имеют различную длину, называют разносторонним треугольником.

Треугольники, изображенные на рисунке 113, − разносторонние. Если сторона равностороннего треугольника равна a, то его периметр вычисляют по формуле:

P = 3 a

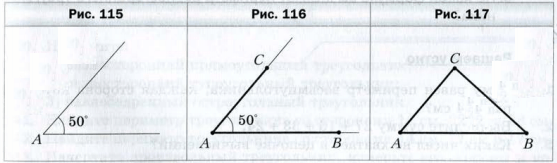
С помощью транспортира построим угол A, градусная мера которого 50 ° (рис. 115 ). На сторонах этого угла от его вершины с помощью линейки отложим отрезок AB длиной 3 см и отрезок AC длиной 2 см (рис. 116 ). Соединив отрезком точки B и C, получим искомый треугольник ABC ( рис. 117 ).

Решение. С помощью линейки строим отрезок AB длиной 2 см (рис. 118 ). От луча AB с помощью транспортира откладываем угол с вершиной в точке A, градусная мера которого равна 40 °. От луча BA в ту же сторону от прямой AB, в которую был отложен первый угол, откладываем угол с вершиной в точке B, градусная мера которого равна 110 °(рис. 119 ).

Найдя точку C пересечения сторон углов A и B, получаем искомый треугольник ABC ( рис. 120 ).

Источник