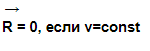Что значит инерциальная система отсчета
Инерциальные системы отсчета.
Инерциальными системами отсчета называют такие системы, относительно которых все тела, не испытывающие действия сил, движутся равномерно и прямолинейно.
Если какая-либо система отсчета движется относительно инерциальной системы поступательно, но не прямолинейно и равномерно, а с ускорением или же вращаясь, то такая система не может быть инерциальной и закон инерции в ней не выполняется.
Во всех инерциальных системах отсчета все механические и физические процессы протекают совершенно одинаково (при одинаковых условиях).
Согласно принципу относительности, все инерциальные системы отсчета равноправны и все проявления законов физики в них выглядят одинаково, а записи этих законов в разных инерциальных системах отсчета имеют одинаковую форму.
Если в изотропном пространстве существует хотя бы одна инерциальная система отсчета, приходим к выводу, что существует бесконечное множество таких систем, движущихся друг относительно друга поступательно, равномерно и прямолинейно. Если инерциальные системы отсчета существуют, то пространство однородно и изотропно, а время – однородно.
Законы Ньютона и другие законы динамики выполняются только в инерциальных системах отсчета.
Рассмотрим пример инерциальной и неинерциальной систем. Возьмем тележку, на которой находятся два шарика. Один из них лежит на горизонтальной поверхности, а другой подвешен на нити. Сначала тележка движется относительно Земли прямолинейно и равномерно (а). Силы, действующие на каждый шарик по вертикали, уравновешены, а по горизонтали на шарики никакие силы не действуют (силу сопротивления воздуха можно проигнорировать).
При любой скорости движения тележки относительно земли (υ1, υ2, υ3 и т.д.) шарики будут находиться в покое относительно тележки, главное, чтобы скорость была постоянной.
Однако, когда тележка наедет на песчаную насыпь (б), ее скорость начнет быстро уменьшаться, в результате чего тележка остановится. Во время торможения тележки оба шарика придут в движение – изменят свою скорость относительно тележки, хотя их никакие силы не толкают.
В этом примере первой (условно неподвижной) системой отсчета является Земля. Вторая система отсчета, движущаяся относительно первой – тележка. Пока тележка двигалась равномерно и прямолинейно, шарики находились в покое относительно тележки, т. е. выполнялся закон инерции. Как только тележка стала тормозить, т. е. начала двигаться с ускорением относительно инерциальной (первой) системы отсчета, закон инерции перестал выполняться.
Строго инерциальной системы отсчета нет. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом, по отношению к которому изучается различных объектов. Все реальные тела движутся с каким-либо ускорением, следовательно любая реальная система отсчета может рассматриваться в качестве инерциальной лишь приближенно.
Инерциальной системой с очень высокой степенью точности считается гелиоцентрическая система, связанная с центром Солнца и координатными осями, направленными на три далекие звезды. Эту систему используют в задачах небесной механики и космонавтики. В большинстве технических задач инерциальной системой отсчета считают любую систему, жестко связанную с землей (или любым телом, которое покоится или движется прямолинейно и равномерно относительно поверхности Земли).
Инерция
Понятие инерция в формулировках Галилея и Ньютона
Галилео Галилей и Исаак Ньютон внесли свой вклад в развитие такого раздела физики, как механика. Неудивительно, что каждый из них предложил свою формулировку.
Галилео Галилей
Исаак Ньютон
Формулировка закона инерции
Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то его движение — равномерно, и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца.
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.
Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела.
Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано.
Варианты формулировки не противоречат друг другу и говорят по сути об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.
Сила: первый закон Ньютона
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Она измеряется в Ньютонах (в честь Исаака Ньютона, разумеется).
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Теперь зная, что такое сила, мы можем вернуться к ньютоновской формулировке закона инерции — он же, Его Величество, первый закон Ньютона:
Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.
Первый закон Ньютона
R — результирующая сила, сумма всех сил, действующих на тело [Н]
const — постоянная величина
В этом законе встречается такое словосочетание, как «система отсчета». Оно изучается в самом начале курса физики, но там это понятие читают в контексте «такие системы отсчета». Напрашивается вопрос: какие такие системы отсчета?
Системы отсчета: инерциальные и неинерциальные
Чтобы описать движение нам нужны три штуки:
В совокупности эти три опции образуют систему отсчета:
Инерциальная система отсчета — система отсчёта, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
Неинерциальная система отсчета — система отсчёта, движущаяся с ускорением.
Рассмотрим разницу между этими системами отсчета на примере задачи.
Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.
Выберите правильное утверждение:
Решение:
Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.
Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.
Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.
Ответ: 1.
Инерция покоя
На столе лежит лист бумаги. На него поставили стакан и резко выдернули лист бумаги из-под него. Стакан почти не двинулся.
То, что стакан остался в состоянии покоя, можно объяснить законом инерции, так как «скорость остается постоянной, в том числе равной нулю». В данном случае инерция покоя — это способность тела сохранять состояние полного механического покоя и «сопротивляться» любым внешним воздействиям. То есть та часть закона инерции, в котором скорость равна нулю.
Так, например, если выбивать пыль из ковра, то в ковер-самолет ваш любимый предмет интерьера не превратится — вместе с пылью не улетит.
Инерция движения
В случае с движением мы берем ту часть первого закона Ньютона, в которой скорость постоянна, но не равна нулю. Здесь мы откроем способность тела к движению, которое было вызвано силой, прекратившей своё действие на тело.
Вернемся к самому началу:
Велосипедист наезжает на камень и падает с велосипеда. Благодаря инерции скорость велосипедиста сохраняется, несмотря на то, что сам велосипед не едет дальше.
Наездник слетает с лошади, если та остановилась. Это тоже происходит из-за инерции — скорость наездника остается постоянной, при этом сама лошадь останавливается.
Мир не идеален
К сожалению, а может быть и к счастью, мы не живем в мире, в котором все тела движутся прямолинейно и равномерно. Из-за этого инерция в реальной жизни невозможна, потому что всегда есть трение, сопротивление воздуха и прочие, препятствующие движению, факторы.
Пуля, вылетевшая из ружья, продолжала бы двигаться, сохраняя свою скорость, если бы на неё не действовало другое тело — воздух. Поэтому скорость пули уменьшается.
Велосипедист, перестав работать педалями, смог бы сохранить скорость своего движения, если бы на велосипед не действовало трение. Поэтому, если педали не крутить — скорость велосипедиста уменьшается, и он останавливается.
Системы отсчета и их виды
В физике часто встречаются термины «система отсчета» и «инерциальная система отсчета». Ознакомимся с ними.
Что такое система отсчета
Система отсчета содержит:
Если все три пункта выполнены, то говорят, что задана система отсчета.
С телом отсчета связаны координатные оси, если тело отсчета будет двигаться, то система отсчета будет передвигаться совместно с ним.
Системы отсчета используются не только в физике. В повседневной жизни мы пользуемся картами местности. При этом, на карте мы отмечаем две точки:
Проложив маршрут и измерив расстояние между этими точками, мы сможем посчитать расстояние, которое нужно преодолеть, чтобы переместиться. А указав интервал времени, мы сможем рассчитать, с кокой скоростью нужно двигаться, чтобы вовремя прибыть к месту назначения.
Виды систем отсчета и их сравнение
Все системы отсчета (сокращенно СО) можно разделить на два вида:
От того, как система отсчета движется, зависит, можно ли считать ее инерциальной, или нет.
Инерциальные системы отсчета
Инерциальная система отсчета — это такая, которая:
Примеры инерциальных систем отсчета:
Примечания:
1. Вместо слов «скорость не меняется», физики часто употребляют такие слова: «скорость постоянная», или «модуль вектора скорости сохраняется».
2. Скорость – это вектор, у любого вектора есть две главные характеристики:
Подробнее о векторах и их характеристиках «здесь».
Не инерциальные системы отсчета
Не инерциальная система отсчета — это такая, которая:
Бывает и так, что одновременно изменяет и по модулю, и по направлению. Главное, что изменяет. Например, гоночный автомобиль на соревнованиях входит в поворот и одновременно набирает скорость.
Примеры не инерциальных систем отсчета:
Для чего нужно знать, к какому виду отнести систему отсчета
Предположим, нам нужно решить какую-то задачу механики. Чтобы ее решить мы вводим систему отсчета. Является ли система отсчета инерциальной, нужно знать потому, что
Для иллюстрации рассмотрим такой пример:
Представим, что мы находимся внутри пассажирского вагона. Поднимем на вытянутой руке мяч и разожмем ладонь, чтобы мяч из нее выпал. Будем изучать траекторию, по которой мяч движется. На всех рисунках пунктиром обозначено начальное положение мяча, а сплошным кругом — его конечное положение. Рассмотрим движение мяча в каждом из случаев:
Случай 1. Вагон покоится
Когда вагон покоится, свободно падающий мяч падает вертикально
Случай 2. Вагон движется равномерно прямолинейно
Красная стрелка — это вектор скорости вагона, он обозначен символом \( \vec
Когда вагон движется равномерно прямолинейно, свободно падающий мяч падает вертикально
Случай 3. Вагон движется прямолинейно равнозамедленно
Вектор скорости вагона обозначен символом \( \vec
Когда вагон движется прямолинейно равнозамедленно, свободно падающий мяч отклоняется от вертикали.
Случай 4. Вагон движется прямолинейно равноускоренно
Вектор скорости вагона \( \vec
Когда вагон движется прямолинейно равноускоренно, свободно падающий мяч отклоняется от вертикали
Случай 5. Вагон движется криволинейно
На рисунке представлена одна из возможных траекторий движения мяча. Траектория мяча будет зависеть от того, будет ли вагон, входящий в поворот, ускоряться, или замедляться.
Изогнутая стрелка указывает направление, в котором вагон поворачивает (изменяет направление движения).
Когда вагон движется криволинейно, свободно падающий мяч отклоняется от вертикали.
Подведем итог:
В первых двух случаях (см. рис. №1, №2), траектории мяча были одинаковыми. В этих двух случаях вагон является инерциальной системой отсчета.
Рисунки №3, №4 и №5 иллюстрируют неинерциальные системы отсчета. В случаях, представленных на этих рисунках, траектории мяча различаются. Формы траекторий зависят от дополнительных сил, действующих в неинерциальных системах отсчета на мяч.
Инерциальная система отсчёта
Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.
Содержание
Свойства инерциальных систем отсчёта
Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.
Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.
Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «C» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.
Связь с реальными системами отсчёта
С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звезд.
Геоцентрическая инерциальная система координат
Применение Земли в качестве ИСО, несмотря на приближённый его характер, широко распространено в навигации. Инерциальная система координат, как часть ИСО строится по следующему алгоритму. В качестве точки O- начала координат выбирается центр земли в соответствии с принятой её моделью. Ось z – совпадает с осью вращения земли. Оси x и y находятся в экваториальной плоскости. Следует заметить, что такая система не участвует во вращении Земли.
Инерциальны ли инерциальные системы отсчёта?
Инерциальны ли инерциальные системы отсчёта?*
Профессор Боряра (Папуа Новая Гвинея)
26 Х 2000 – когда-то в 2005 г.
В многочисленных монографиях, статьях и учебниках физики инерцальные системы отсчёта (ИСО) определяются обычно так:
«Система отсчёта, в которой справедливы законы Ньютона»
Примеры схожих определений ИСО:
«. мы вводим понятие инерциальной системы; оно призвано означать систему координат, в которой закон инерции выполняется в своей оригинальной форме.
Существует бесконечное число эквивалентных систем, называемых инерциальнымии и совершающих поступательное движение (равномерное и прямолинейное) относительно друг друга, в которых законы механики выполняются в своей простой классической форме».
М. Борн, Эйнштейновская теория относительности, стр.91-92.
«Система отсчёта, в которой тело, не испытывающее действия сил, движется без ускорения, называется инерциальной».
В. Пановски, М. Филлипс, Классическая электродинамика, стр.253
«Системы отсчёта, в которых свободная материальная точка движется равномерно и прямолинейно. Подобная ситстема отсчёта называется инерциальной, а утверждение о возможности найти такую систему составляет содержание закона инерции.»
«По отношению к одной инерциальной системе можно определить бесконечное множество других инерциальных систем, движущихся с постоянной скоростью и полученных в результате преобразований Галилея»,
М.А.Тоннела, Основы электромагнетизма и теории относительности, стр.107-108
«Систему координат, состояние движения которой таково, что относительно неё выполняется закон инерции, мы называем «Галилеевой системой координат» Законы механики Галилея-Ньютона применимы только для галилеевой системы координат»
А.Эйнштейн, О специальной и общей теории относительности.
«Такие системы координат, в которых все ускорения обусловлены действием каких-либо тел, носят название «инерциальных систем координат»»,
С.Э. Хайкин, Физические основы механики, стр.121.
«Существуют системы отсчёта, в которых свободное движение тел, т.е. движение тел, не находящихся под действием внешних сил, происходит с постоянной скоростью. Такие системы носят название инерциальных».
Л.Д. Ландау, Е. М Лифшиц, Теория поля, стр. 9
Этот список цитат можно было бы продолжить
Часто можно заметить, что слова «система отсчёта» заменяются словами «система координат» и оба эти термина используются, как синонимы, равноправные, равнозначащие и тождественные.*
На наш взгляд такое отождествление не вполне корректно. Система координат – это, в первую очередь, чисто математическое понятие, со всей присущей ему абстрактностью. Система же отсчёта – понятие физическое, и представляет собой не просто некую систему координат, а означенную систему, «жёстко» связанную с материальным телом или материальным объектом», т.е. никак не отвлечённое математическое понятие, «состоящее» из трёх жёстко скреплённых друг с другом осей и часов. Разница между этими определениями не столь уж мала и несущественна, сколь может показаться на первый взгляд.
В общем, определение ИСО это: «Система отсчёта, в которой соблюдаются законы Ньютона. Определив таким образом одну ИСО, мы можем обнаружить множество аналогичных систем, если эти системы движутся равномерно и прямолинейно относительно вышеуказанной. Такие системы отсчёта также можно считать инерциальными.»
Вот это-то последнее утверждение я попытаюсь оспорить, иными словами, для меня определением ИСО является лишь первая часть, выделенная прописным (Italic) шрифтом, которая фактически включает в себя и Общий Принцип Относительности: ведь, если в свободно падающем в поле тяготения лифте выполняются законы Ньютона, то и такую систему отсчёта можно считать ИСО.
Я же сейчас разберу понятия «систем отсчёта, движущихся равномерно и прямолинейно относительно нашей исходной, уже определённой выше ИСО». Я хочу показать, что выражение «движущиеся равномерно и прямолинейно относительно ИСО» заключает в себе неявную ошибку, а именно: фактически речь идёт не о системе, движущейся «относительно этой ИСО», а относительно некоего стороннего наблюдателя, «Божественного ока», жёстко связанного с Абсолютным и неподвижным Ньютоновским пространством, с Неподвижным Эфиром, с неподвижной сферой бесконечно удалённых звёзд и т.п. «абсолютами».
Итак, мы видим противоречие: Оба наблюдателя установили (и совершенно верно), что их системы – это ИСО (по Ньютону). А их взаимное движение (по их же измерениям) показывает, что каждый из них движется неравномерно и непрямолинейно по отношению к другому!
Таким образом возникает возможность абсурдного, внутренне противоречивого «кинематического» определения инерциальных систем:
Две инерциальные системы – это два множества упорядоченно расположенных точек, движущихся в совокупности равномерно и прямолинейно друг относительно друга, в то время, как взяв любую пару точек, принадлежащих этим множествам (по одной из каждого множества) мы обнаружим, что каждая из них движется не равномерно и не прямолинейно по отношению к другой..
Укрепим на параллельных осях двух ИСО цепочку лампочек, поставленных на равных расстояниях друг от друга. И попытаемся таким методом установить равномерность их взаимного движения. Скажем, по равномерности темпа попадания лампочек в окуляр прибора в другой системе. Во-первых – где гарантия, что они расположены именно так, а не иначе? Со слов наблюдателя в этой системе7 Но физика не строит свои фундаментальные понятия «на честном слове». Во вторых – он может и ошибаться – находясь в свободно падающем в поле тяготения лифте. И тогда неравномерно поставленные лампочки вне его лифта, (паралельно траектории его падения) могут у него создать иллюзию равномерности движения его лифта. В третьих – получается, что мы не можем, находясь в одной системе, установить (без подсказки), как движется другая система, где, допустим, нет сотрудничающего с нами наблюдателя. В-четвёртых: инфинитные системы хороши в математике, но принципиально неприемлемы в физике – иначе надо ввести бесконечную скорость распространения сигнала, что противоречит СТО.
Таким образом мы видим, что «кинематическое добавление» в определении инерциальных систем отсчёта неявно проводит в физику всё ту же идею Абсолютного Неподвижного Пространства, или идею любого другого Абсолюта, вроде Божественного Наблюдателя. Поэтому, на наш взгляд, эту кинематическую добавку следует отбросить и определять ИСО лишь опираясь на «динамический» способ, т.е. системы, в которых выполняются законы Ньютона и ничего более!