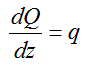Что вызывает скачек на эпюре изгибающих моментов

iSopromat.ru

1. Проверка по “скачкам”

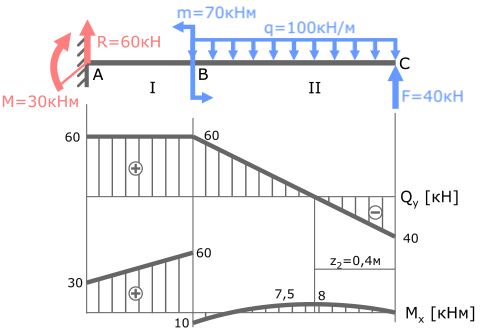
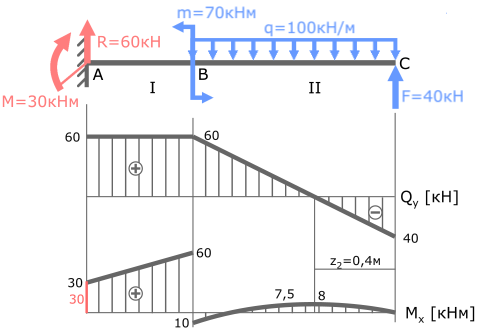
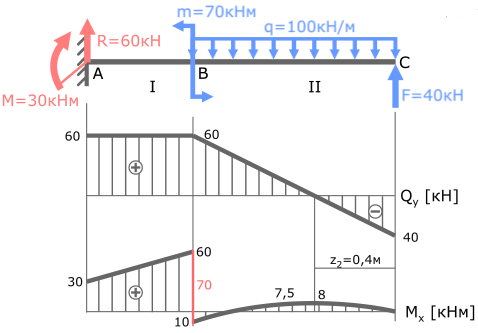
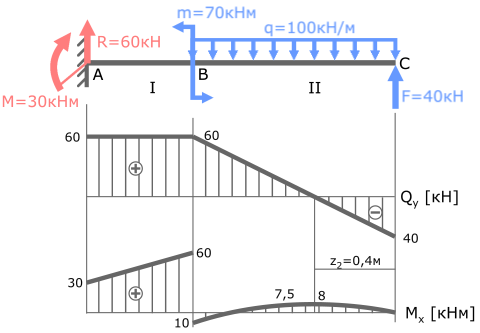
В сечениях балки, где приложен изгибающий момент, на эпюре M будет скачок.

Здесь к балке приложено два момента: M в точке A и m в точке B.

Проверим наличие скачков в указанных сечениях:

В точке A изгибающий момент M равен 30кНм.
Скачок значений на эпюре M также равен 30.

2. Проверка дифференциальной зависимости dM/dz=Q

Выполним проверку эпюры по дифференциальной зависимости dM/dz=Q.

На участках балки, где эпюра Q параллельна базовой линии (I с.у.) эпюра M имеет вид прямой наклонной линии.

На участках балки с распределенной нагрузкой, где Q≠const (II с.у.) эпюра моментов M имеет вид параболы.

В сечении, где эпюра Q пересекает базовую линию, на эпюре M_x определяется экстремум.

Все условия выполнены, значит, эпюра M_x построена правильно.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

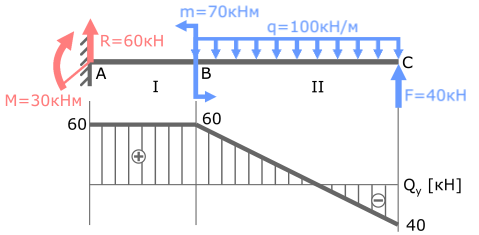
Проверка правильности построения эпюр внутренних поперечных сил Q_y выполняется по “скачкам” и дифференциальной зависимости dQ/dz=q.

Перед тем как строить эпюру изгибающих моментов, необходимо убедиться в том, что связанная с ней эпюра внутренних поперечных усилий построена правильно.

Эпюры поперечных сил Q проверяются по “скачкам” и дифференциальной зависимости dQ/dz=q.

1. Проверка по “скачкам”

При изгибе, в сечениях балки, где приложена сосредоточенная сила, на эпюре Q должен быть скачок на величину этой силы.

В данном случае к балке приложены две силы: реакция опоры R (в точке A) и сила F (в т. C).

Проверяем в указанных точках наличие скачков на эпюре Q:

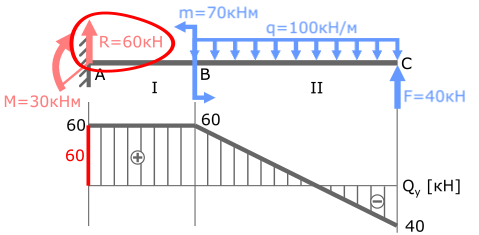
В точке A сила R=60кН, скачок значения Q в этом сечении тоже равен 60кН.

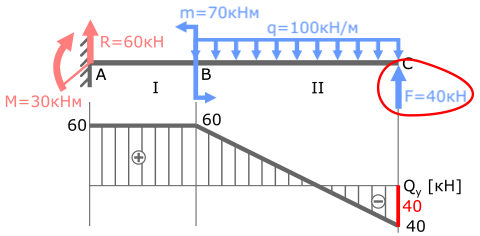
В точке C поперечная сила F=40кН, скачок соответственно составляет 40кН.

В точке B сосредоточенных поперечных сил нет, поэтому скачка на эпюре Q там быть не должно.

Здесь на всякий случай напомним, что изгибающие моменты на эпюру Q никак не влияют.

2. Проверка по дифференциальной зависимости

показывает что на участках балки, где нет распределенной нагрузки q (I с.у.) Q=const, т.е. линия эпюры Q располагается параллельно базовой линии или совпадает с ней (в случае, когда Q=0).

На участках где распределенная нагрузка есть (II с.у.) значение Q будет переменным.

При этом, если нагрузка q распределена равномерно на эпюре Q будет прямая наклонная линия, и чем больше величина нагрузки q тем больше угол между линией эпюры Q и базовой линией.

Разность значений Q на границах участка должна быть равна произведению интенсивности q на длину соответствующего силового участка.

В случае, когда нагрузка распределена неравномерно эпюра Q будет иметь вид параболы.

Если все эти условия выполняются, значит, эпюра внутренних поперечных сил построена правильно.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Когда в эпюре изгибающих моментов в сечении возникают скачки?

+ Если в этом сечении приложен сосредоточенный момент

— Если в этом сечении приложена сосредоточенная сила

— Если в этом сечении приложена распределенная нагрузка

— Если в этом сечении изменяются геометрические характеристики

Когда в эпюре поперечных сил возникают скачки?

+ Если в этом сечении приложена сосредоточенная сила

— Если в этом сечении приложен сосредоточенный момент

— Если в этом сечении приложена распределенная нагрузка

— Если в этом сечении изменяются геометрические характеристики

В каком сечении в эпюре изгибающих моментов возникает экстремум?

+ В том сечении, где поперечная сила имеет нулевое значение

— В том сечении, где поперечная сила имеет максимальное значение

— В том сечении, где поперечная сила имеет минимальное значение

— В том сечении, где внешняя нагрузка имеет максимальное значение

— В том сечении, где внешняя нагрузка имеет минимальное значение

Как определяются реакции опор в простой балке?

— Из уравнения равновесия внешних сил

— Из кинематических уравнений

— Из условий закрепления

Изгибающий момент в балке вызван действием каких напряжений?

+ Нормальных напряжений в поперечном сечении

— Касательных напряжений в поперечном сечении

— Нормальных напряжений в продольном сечении

— Касательных напряжений в продольном сечении

При чистом кручении используется следующее допущение

+ поперечные сечения плоские до деформации остаются плоскими после деформации(гипотеза Бернулли)

— гипотеза прямых нормалей

— расстояния между поперечными сечениями изменяются

— радиус поперечного сечения изменяется

При чистом кручении углы поворота сечений определяются по формуле

где величина означает

+ жесткость при кручении

— жесткость при изгибе

— жесткость при растяжении-сжатии

— жесткость при изгибно-крутильных деформациях

Касательные напряжения при чистом кручении определяются по формуле , где означает

+ расстояние от точки до центра тяжести

Касательное напряжение при чистом кручении для круглого сечения определяется по формуле

Максимальные значения имеют место

+ в точках по окружности

— в середине радиуса

— в четверти радиуса

определяет

+ касательные напряжения при чистом кручении

— нормальные напряжения при кручении

— касательные напряжения при поперечном изгибе

— касательные напряжения при сдвиге

Следующее условие прочности записывается при

Условие прочности при кручении записывается в виде: . Величина W_p означает

+ полярный момент сопротивления

— момент сопротивления при изгибе

— осевой момент инерции

— статический момент сечения

Момент инерции сечения, определяемый по формуле:

относится к сечению в виде

Следующая формула для нормальных напряжений

— при чистом кручении

— при поперечном изгибе

Определите формулу напряжения в поперечном сечении круглого стержня при кручении.

+

—

—

—

Укажите формулу угла поворота сечения при кручении.

+

—

—

—

Условие прочности при кручении круглых стержней.

+

—

—

—

Эпюра поперечных сил при изгибе балки, это:

+ Графическая зависимость изменения поперечных сил по длине балки

— Дифференциальная зависимость от нормальных напряжений

— Графическая зависимость изменения изгибающих моментов по длине балки

— Функциональная зависимость от изгибающего момента

Эпюра изгибающих моментов при изгибе балки, это:

+ Графическая зависимость изменения изгибающего момента по длине балки

-Функциональная зависимость касательных напряжении от изгибающего момента

— Графическая зависимость изменения поперечных сил по длине балки

-Функциональная зависимость нормальных напряжении от изгибающего момента

По какой формуле определяются нормальные напряжения при чистом изгибе?

+

—

—

—

Какие напряжения возникают при действии поперечной нагрузки для стержня сплошного поперечного сечения?

+ Нормальные и касательные

— Только нормальные напряжения

— Только касательные напряжения

По какой формуле определяется касательное напряжение при изгибе?

+

—

—

—

Как изменяются касательные напряжения по высоте балки сплошного поперечного сечения при изгибе?

+ Наибольшие напряжения будут на нейтральной оси сечения, а на контуре сечения они равны нулю

— Наибольшие напряжения будут в точках сечения, наиболее удаленных от нейтральной оси сечения, а на нейтральной оси они равны нулю

— Касательные напряжения равны нулю

Укажите формулу касательного напряжения ( ) при изгибе.

+

—

—

—

Какой изгиб называется чистым?

— Изгиб, при котором в поперечных сечениях балки возникают поперечная сила и изгибающий момент

— Изгиб, при котором в поперечных сечениях балки не возникает ни одно из внутренних усилий

Укажите формулу нормального напряжения при чистом изгибе.

+ — — —

Укажите формулу Журавского при изгибе.

+ — —

—

Где расположено опасное сечение балки при изгибе?

+ Там, где действует максимальный изгибающий момент

— Там, где действует максимальная поперечная сила

— Там, где действует постоянная поперечная сила

— Там, где изгибающий момент равен нулю

Какие напряжения возникают при чистом кручении валов?

— Нормальные и касательные

В формуле для сдвига фаз величины ω, θ означают

+ Частоты собственной и вынужденной колебаний для системы с одной степенью свободы

— Частоты собственных и вынужденных колебаний для системы с распределенной массой

— Частоты собственной и вынужденной колебаний для системы с конечным числом степеней свободы

— Частоты собственной и вынужденной колебаний для системы с двумя степенями свободы

Источник

Построение эпюр поперечной силы и изгибающего момента для балок. Часть 2

Построить эпюры Q_y и М_х для простой консоли, изображенной на рисунке.

1. Определение опорных реакций. Составляем уравнения равновесия:

2. Построение эпюр поперечной силы и изгибающего момента.

Э п ю р а М_х. В сечении А приложен момент М_А, вызывающий растяжение верхних волокон, поэтому на эпюре изгибающего момента происходит скачок вверх на величину момента M_A = 6qa 2.

На участке DE изгибающий момент изменяется по закону квадратной параболы, обращенной выпуклостью вниз (в сторону погонной нагрузки q). В сечении Е по условию загружения балки М_Е = 0. По двум точкам D и Е приближённо стр

1. Определение опорных реакций. Составляем уравнения равновесия:

, R_Ba + qa2 +3qa2-qaa = 0,

2. Построение эпюр поперечной силы и изгибающего момента.

Э п ю р а Q_y. Строится по формуле Q_y = Q_o ± qz. В данном случае перед вторым слагаемым следует взять знак “плюс”, так как погонная нагрузка положительна (см. правила построения эпюр). На участках АВ и ВС эпюра Q_y изображается прямой, наклоненной вверх (в направлении погонной нагрузки q), а на участке CD поперечная сила постоянна (q = 0). В сечениях В и D на балку действуют сосредоточенные силы R_A и R_D, поэтому на эпюре Q_y возникают скачки. Вычисляем значения поперечной силы в характерных точках Q_A = 0,

По заданной эпюре поперечной силы Q_y установить нагрузку, действующую на двухопорную балку, и ее опорные реакции. Построить также эпюру изгибающего момента, учитывая, что на правой опоре С приложена пара сил.

откуда M_C = 2qa 2 и направлен против часовой стрелки.

Эпюру М_х строим по формуле М_х = М_о + . На участке АВ изгибающий момент изменяется по квадратичному закону. На концевой шарнирной опоре А нет пары сил, поэтому М_А = 0. В сечении, где Q_y = 0, изгибающий момент принимает экстремальное значение:

По заданной эпюре изгибающего момента построить эпюру поперечной силы и определить нагрузку, действующую на балку. Криволинейный участок эпюры М_х очерчен по квадратной параболе, а кружком отмечена ее вершина.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.1).

1) Проведем две оси, параллельные оси балки (одну для эпюры Q_Y, вторую для эпюры M_X).

2) Балка имеет один участок загружения.

3) Строим эпюру Q_Y. Сделаем сечение (1), отбросим жесткую заделку. Учитывая правило знаков, получим . В сечении (2) получим . Силы , так как сила F поворачивает оставшуюся часть балки вокруг сечения по часовой стрелке (рис.2,а).

Положительные значения поперечной силы откладывают всегда выше оси

Соединим их прямой линией, поставим знак, эпюру заштрихуем, обозначим.

4) Строим эпюру М_Х. Сделав сечение и отбросив часть с жесткой заделкой, сосчитаем момент от силы F относительно сделанного сечения. Получим . Для эпюры изгибающих моментов принимается следующее правило: значения моментов откладываются от оси в сторону растянутого волокна. Из рис.2,б, следует, что сила F растягивает верхние волокна, поэтому полученное значение М_Х откладываем выше оси. Соединяем отложенные значения прямой линией. Знак на эпюре изгибающих моментов можно не ставить. Эпюру штрихуем и обозначаем (рис.1).

5) Проверка эпюр. К балке не приложена распределенная нагрузка, следовательно, на графиках Q_Y и М_Х имеем прямые линии, причем на эпюре Q_Y это прямая, параллельная оси. На свободном конце балки приложена сосредоточенная сила F = 6кН в этом сечении на эпюре Q_Y образовался скачок, равный 6.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Проводим оси для построения эпюр.

2) Делим балку на два участка загружения.

Откладываем значения ниже оси, соединяем прямой линией.

Значение откладываем ниже оси, соединяем прямой линией.

Ставим знаки, эпюру штрихуем и обозначаем.

Откладываем значения ниже оси, так как сила F растягивает нижние волокна, соединяем прямой линией.

Значения откладываем ниже оси и соединяем параболой. При этом выпуклость параболы должна быть обращена в сторону действия распределенной нагрузки. Это правило называют «правилом паруса». Роль паруса здесь играет эпюра, а роль ветра – нагрузка.

5) Проверка эпюр. На участке балки с распределенной нагрузкой получаем на эпюре Q_Y наклонную прямую, на эпюре M_X – параболу. В сечении с приложенной сосредоточенной силой F = 8 кН на эпюре Q_Y образовался скачек равный 8.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Проводим оси для построения эпюр.

2) Делим балку на два участка загружения.

Откладываем значения ниже оси, соединяем прямой линией.

Откладываем ниже оси, а — выше оси, соединяем прямой линией (см. рис.).

Откладываем ниже оси, соединяем с нулем прямой линией.

Из рисунка следует, что эпюра поперечных сил Q_Y на этом участке пересекает ось, то есть в некотором сечении (5) сила . Отсюда следует, что в сечении (5) изгибающий момент М_Х достигает экстремального значения (максимума или минимума). Таким образом, на этом участке следует просчитать момент в трёх точках.

Определим экстремальное значение момента. Выясним сначала, на каком расстоянии Z от правой границы участка находится сечение (5), в котором поперечная сила равна нулю.

Найдем значение момента.

Откладываем значения ниже оси и соединяем параболой по правилу «паруса», то есть выпуклостью вниз (см. рис.).

5) Проверка эпюр. Все линии на эпюрах соответствуют приложенным нагрузкам, силе F = 8 кН соответствует скачок, равный 8 на эпюре Q_Y.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис. 1).

1) Расчёт балки с шарнирным закреплением следует начинать с определения реакций связей. Расставим эти реакции. В шарнирно –подвижной опоре А возникает одна вертикальная реакция R¢_A. В шарнирно-неподвижной опоре В, вообще говоря, возникает две реакции – вертикальная R¢_B и горизонтальная Н_В, однако, поскольку в случае вертикального плоского изгиба все силы действуют перпендикулярно оси балки, горизонтальная реакция Н_В всегда будет равна нулю, поэтому в дальнейшем показывать ее на схеме балки не будем. Вертикальные реакции найдем из уравнений статики.

При записи уравнений использовалось следующее правило знаков: если сила поворачивает балку вокруг т.А (т.В) по часовой стрелке, то момент от этой силы берется со знаком «+».

Для проверки найденных реакций используем уравнение статики: (сумма всех вертикальных сил должна быть равна нулю). При этом силы, изображенные на схеме балки направленными вверх, берем со знаком «+».

Подставим сюда найденные значения реакций со своими знаками.

— 23 + 10 × 2 + 15 – 12 = 0; 35 – 25 =0; 0 = 0.

Поскольку направления вертикальных реакций поначалу были взяты произвольно, то полученные в результате знаки «-» у реакций R_A, R_B показывают, что мы не угадали направление реакций, в действительности они направлены вниз. Удобно изменить направление этих реакций на обратное и в дальнейшем считать эти реакции положительными (см. рис.1).

2) Проводим оси для построения эпюр.

3) Делим балку на три участка загружения.

(отбросили правую часть балки),

(отбросили левую часть балки).

Пару сил М = 20 кНм при вычислении Q_Y, естественно, не учитываем.

Откладываем значения от оси, соединяем прямой линией.

;

;

;

Чтобы не ошибиться в знаке изгибающего момента, сечение, в котором он определяется, следует представлять защемленным, а опоры – отброшенными (рис.2):

Откладываем значения от оси и соединяем параболой по правилу «паруса», то есть направленной выпуклостью вверх.

Откладываем значения выше оси, соединяем прямой линией.

Отложенные от оси значения соединяем прямой линией (рис.1).

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Найдем реакции опор R_A, R_B.

Обе реакции получились положительными, то есть мы угадали их направление, они действительно направлены вверх.

2) Балка имеет два участка загружения.

;

Откладываем значения от оси и соединяем прямой линией.

;

Откладываем значения от оси и соединяем прямой (см. рис.).

Из эпюры сил следует, что на этом участке будет возникать экстремальный момент, поэтому будем определять М_Х в трёх сечениях. (отбрасываем правую часть балки); (отбрасываем левую часть балки).

Находим координату Z сечения (5):

Находим экстремальный момент.

Откладываем значения от оси и соединяем параболой по правилу «паруса», то есть выпуклостью вниз.

Отложенные от оси значения соединяем прямой (см. рис.).

Линии эпюры соответствуют приложенным нагрузкам. К балке приложены три сосредоточенные силы – R_A, F, R_B на эпюре Q_Y в соответствующих сечениях имеем скачки.

К балке на опоре В приложена пара сил М: на эпюре М_Х имеем на правом конце скачок, равный М = 48.

Дана балка с действующими на нее нагрузками (рис. а). Требуется определить внутренние усилия – поперечную силу Q и изгибающий момент М в балке, построить графики их изменения вдоль оси стержня (эпюры Q и М).

Прежде всего найдем опорные реакции. Балка имеет жёсткое защемление на правом конце (В балке с заделкой можно строить эпюры Q и М без определения опорных реакций, рассматривая все силы с одной стороны от сечения – со свободного конца. Но студенту, только начинающему осваивать построение эпюр, рекомендуем все же реакции находить. Это дополнительная проверка правильности решения задачи) и в этом закреплении при заданной вертикальной нагрузке возникают две опорные реакции: вертикальная реакция R_A и реактивный момент M_A. Горизонтальная реакция при действии вертикальной нагрузки равна нулю. Это следует из уравнения равновесия «сумма проекций всех сил на горизонтальную ось равна нулю». Определим R_A и M_A, используя два других уравнения статики. Желательно составлять такие уравнения, в каждое из которых входит только одна неизвестная. В данном случае такими уравнениями являются «сумма проекций всех сил на вертикальную ось (ось z) равна нулю» и «сумма моментов всех сил относительно точки А равна нулю»:

;

;

Из первого уравнения найдем R_A = 30 кН, из второго – М_А =5 кНм. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: R_A – вверх, а М_А – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например

– 30×2 – 15×2×1 – 60 + 10×1×2,5 + 30×4+5 = – 150 + 150 = 0.

Теперь определяем внутренние усилия: поперечную силу Q и изгибающий момент М. В соответствии с методом сечений рассекаем балку на каждом участке (в данной задаче их три) произвольным сечением и рассматриваем все силы, расположенные с одной стороны от сечения: слева или справа. Удобно рассматривать все силы с той стороны от сечения, где сил меньше. Начало отсчета координаты x на каждом участке можно выбирать произвольным образом. Например, на рис. а начало отсчета x на каждом участке – свое и находится в начале участка. Запишем выражения для Q и М на каждом участке.

Рассмотрим силы, расположенные слева от сечения. По определению поперечной силы и с учетом правила знаков для Q :

Здесь q₁x₁ – равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.

По определению изгибающего момента и с учетом правила знаков для М :

где во втором слагаемом x₁/2– плечо равнодействующей равномерно распределенной нагрузки (q₁x₁), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x₁).

Для построения эпюр найдем значения Q и М на границах участка:

Участок 2:

Снова рассмотрим все силы, расположенные слева от сечении

Граничные значения Q и М:

в начале участка (x₂ = 0) ; ,

в конце участка (x₂=b) ; .

Участок 3: .

Теперь рациональнее рассмотреть все силы справа от сечения. Тогда

Из этих выражений следует, что поперечная сила на третьем участке – постоянная величина, а изгибающий момент меняется по линейному закону и на границах участка имеет следующие значения:

в конце участка (x₃=c) .

Запишем результаты определения внутренних усилий в таблицу, сосчитав численные значения Q и М на границах участков (табл. 1).

Из таблицы видно, что поперечная сила на первом участке меняет свой знак, т. е. график Q пересекает нулевую линию. Это значит, что изгибающий момент на этом участке имеет экстремум. Найдем максимальное значение М на этом участке. Сначала определим то значение координаты х₁, при котором поперечная сила равна нулю. Обозначим это значение координаты х₀ (см. рис. ).

х0 = 1,33 м.

Чтобы найти максимальное значение изгибающего момента, подставим х₀ в выражение для М на первом участке:

кНм.

По результатам вычислений в таблице строим эпюры Q и М на каждом участке (см. рис. б). Не забываем после построения эпюр проанализировать результаты по тем правилам проверки правильности построения эпюр, которые перечислены ранее.

На балку кроме равномерно распределенной нагрузки действует линейно распределенная (треугольная) нагрузка (рис. а). Построим эпюры распределения поперечной силы и изгибающего момента, обращая внимание на определение Q и М на участке с треугольной нагрузкой.

Найдём опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций R_A и R_B (горизонтальная реакция H_A = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:

;

;

;

Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).

Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки, расположенной слева от рассматриваемого сечения на участке длиной х₂, определим интенсивность распределенной нагрузки в сечении х₂, которая на рис. а обозначена q_x. Для этого составим пропорцию: , откуда . Тогда равнодействующая этой распределенной нагрузки на участке длиной х₂ . Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен , где – плечо равнодействующей.

Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х₀ на этом участке (рис. б). Определим величину х0, приравняв выражение для поперечной силы на втором участке нулю:

, откуда x_{0 = 2,89 м. Тогда}

По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором участке можно определить по знаку второй производной . В данном случае функция q(x) является убывающей, следовательно , а . Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q_(x) должен равняться нулю, так как в этом сечении dQ/dx=0. Это возможно тогда, когда функция Q_(x) имеет выпуклость вниз.

После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.

Построить эпюры M_x и Q_y для заданной балки (см. рис.).

1.Предположим, что опорные реакции А и В направлены вверх (рис. а). Из уравнений равновесия имеем:

А_H = 0

B_{v = 40 н;}

A_{v = 60 н;}

Для проверки найденных реакций используем уравнение равновесия.

Уравнение тождественно удовлетворяется, что указывает на правильность определения опорных реакций.

2. Для построения эпюр M_x и Q_y заданную балку разобьем на участки I, II, III таким образом, что бы в пределах каждого участка силовой фактор определялся непрерывной функцией от z. Применим метод сечений к I и III участкам (рис. б). Выражения для внутренних силовых факторов имеют вид:

Проверим выполнение дифференциальных зависимостей на построенных эпюрах Q_y, M_x. На участках I, II производная положительная функция (M_x) возрастает. В сечении D производная (Q_y) имеет скачок, а функция (M_x) имеет излом. В сечении z₃ = z₀ производная (Q_y) равна нулю, функция (M_x) достигает максимума на III участке.

Задачи для самостоятельного решения

Построить эпюры поперечных сил и изгибающих моментов для балок, защемленных одним концом и загруженных, как показано на рисунке. Подсчитать наибольшие по абсолютному значению величины поперечных сил и изгибающих моментов, если F =20 кН, q =20 кН/м, М₀ = 40 кН/м и l =2 м

Построить эпюры поперечных сил и изгибающих моментов для балок на двух опорах, загруженных, как показано на рисунке. Найти mах Q и mах М при следующих данных: F= 60 кН, q =20 кН/м, М₀=60 кНм, l =3 м.

При каком значении силы F изгибающие моменты в опорных сечениях балок, изображенных на рисунке, будут равны нулю? Построить эпюры Q и М при этих значениях сил.

Построить в общем виде эпюры Q_Y и M_X для заданной балки.

Построить эпюры поперечных сил и изгибающих моментов, если L₁=0,2м; L₂=0,3м; q=4 кН/м.

Для изображенного стержня, определить внутренние усилия в сечениях А и В.

Для всех стержней, изображенных ниже, определить вид деформации и построить эпюры соответствующих внутренних усилий. Для самоконтроля приведены уже построенные эпюры.

Источник