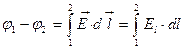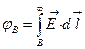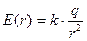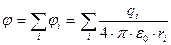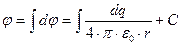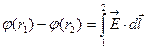Что выражает расчетная формула
Основные понятия и расчетные формулы



Старооскольский технологический институт им. Угарова А.А.
(филиал) Федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский технологический университет «МИСиС»
Кафедра металлургии и металловедения им. Угаровой С.П.
ТЕПЛОМАССООБМЕН
для практических занятий
бакалавриата по направлению
13.03.01 – «Теплоэнергетика и теплотехника»
Старый Оскол 2017 г.
РАЗДЕЛ 1.ТЕПЛОПРОВОДНОСТЬ.. 4
1.1. Основные понятия и расчетные формулы.. 4
1.2. Теплопроводность при стационарном режиме. 8
1.2.1. Передача тепла через плоскую стенку. 8
а) Граничные условия 1 рода. 8
б) Граничные условия III рода. 12
в) Смешанные граничные условия. 14
1.2.2. Передача тепла через цилиндрическую стенку. 15
а) Граничные условия I рода. 15
б) Граничные условия III рода. 20
1.2.3. Передача тепла через оребренные поверхности. 22
1.3. Теплопроводность при нестационарном режиме. 24
1.3.1. Неограниченная пластина. 25
1.3.2. Цилиндр бесконечной длины.. 27
1.4. Примеры решения задач. 30
РАЗДЕЛ 2. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ. 35
2.1. Виды лучистых теплообменов. 35
2.2. Законы теплового излучения. 41
2.3. Угловые коэффициенты излучения. 44
2.4. Свойства угловых коэффициентов излучения. 45
2.5. Теплообмен излучением между твердыми телами, разделенными лучепрозрачной средой 46
2.5.1. Теплообмен излучением в системе тел с плоскопараллельными поверхностями 47
2.5.1.1. Излучающая система без экранов. 47
2.5.1.2. Теплобмен излучением при наличии экранов. 48
2.6. Теплообмен излучением между телом и его оболочкой.. 50
2.6.1. Излучающая система без экранов. 50
2.6.2. Теплообмен излучением при наличии экранов. 51
2.7. Теплообмен излучением между двумя телами, произвольно расположенными в пространстве 53
2.8. Излучение изотермической полости.. 53
2.9. Теплообмен в поглощающих и излучающих средах. 54
2.10. Примеры решения задач. 57
РАЗДЕЛ 3. КОНВЕКТИВНЫЙ ТЕПЛО- И.. 58
3.1. Основные понятия и определения. 58
3.2. Свободная конвекция. 60
3.3. Вынужденная конвекция. 63
3.3.1. Конвективный теплообмен при движении жидкости (газа) в трубах 63
3.3.2. Конвективный теплообмен при внешнем обтекании тел. 65
3.3.4. Теплоотдача на плоской поверхности при вынужденном течении в случае турбулентного пограничного слоя 74
3.3.5. Вынужденная теплоотдача при течении жидкости в трубах 75
3.3.6. Теплоотдача при поперечном обтекании одиночной трубы потоком жидкости 79
3.3.7. Обтекание шара. 81
3.4. Ориентировочные значения коэффициента теплоотдачи.. 81
3.5. Массоперенос. 82
3.6. Примеры решения задач. 84
а) Основная литература: 88
б) Дополнительная. 88
в) электронный контент: 88
Введение
В результате освоения дисциплины «Теплофизика» обучающийся должен:
-использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования процессов тепломассообмена (ОК-6)
-сочетать теорию и практику для решения инженерных задач по процессам передачи тепла (ПК-4)
-использовать физико-математический аппарат для решения задач тепломассопереноса, возникающих в ходе профессиональной деятельности (ПК-20);
-использовать основные понятия, законы и модели термодинамики, переноса тепла и массы (ПК-21)
РАЗДЕЛ 1.ТЕПЛОПРОВОДНОСТЬ
Основные понятия и расчетные формулы
¨ Теплопроводность определяется тепловым движением микрочастиц тела, т.е. движением микроструктурных частиц вещества (молекул, атомов, ионов, электронов).
¨ Температурное поле — совокупность значений температур в данный момент времени для всех точек этого пространства.
¨ Стационарное температурное поле — это поле, в котором температура является функцией только пространственных координат f(x, y, z).
¨ Нестацонарное температурное поле или неустановившееся — поле, температура в каждой точке которого зависит, не только от координат, но и от времени, т.е.
 | (1.1) |
¨ Геометрическое место точек, имеющих одинаковую температуру, называют изотермической поверхностью.
¨ Предел отношения изменения температуры t к расстоянию между изотермами по нормали n называют температурным градиентом:
 | (1.2) |
¨ Температурный градиент — вектор, направленный по нормали к изотермической поверхности, причем, за положительное направление вектора принимается направление в сторону возрастания температуры, т.е. 
¨ Количество тепла Q, проходящее в единицу времени через изотермическую поверхность F, называют тепловым потоком.
¨ Тепловой поток q на 1 м 2 поверхности называют удельным тепловым потоком, плотностью теплового потока или тепловой нагрузкой поверхности нагрева
 . . | (1.3) |
Величины q и Q являются векторами, направленными по нормали к изотермической поверхности, причем, за положительное направление принимается направление в сторону уменьшения температуры. Векторы теплового потока и градиента температуры противоположны.
Линии, касательные к которым совпадают с направлением вектора теплового потока, называют линиями теплового потока. Эти линии перпендикулярны к изотермическим поверхностям (см. рис.1.2).
Основной закон теплопроводности — закон Био-Фурье является феноменологическим описанием процесса и имеет вид:
 , , | (1.4) |
q — удельный тепловой поток, Вт/м 2 ;
λ — коэффициент теплопроводности вещества, Вт/(м × К);
grad t — градиент температуры, K/м.
Знак «минус» в уравнении (1.4.) поставлен потому, что тепло распространяется в сторону падения температуры и, следовательно, приращение температуры в этом направлении имеет отрицательное
Общее количество тепла, переданное теплопроводностью через стенку поверхностью F, м 2 за время t, составит
 . . | (1.5) |
¨ Величина коэффициента теплопроводности зависит от природы тел и их температуры. Для большинства материалов эта зависимость линейная
 , , | (1.6) |
lt, l0 — значения коэффициента теплопроводности соответственно при 0 °С и при t °С;
b — постоянная, определяемая опытным путем.
Наихудшими проводниками тепла являются газы, для них λ = 0,006 — 0,6 Вт/(м × К). Для чистых металлов коэффициент теплопроводности находится в диапазоне 12 — 420 Вт/(м × К). Примеси к металлам вызывают уменьшение коэффициента теплопроводности. Из металлов самым теплопроводным является серебро.
Пористые материалы, плохо проводящие тепло называются теплоизоляционными. Для них λ = 0,02 — 0,23 Вт/(м × К) (например: асбест, шлаковая вата, диатомит и др.)
¨ Весь класс явлений теплопроводности описывается в общем виде дифференциальным уравнением теплопроводности, которое имеет вид:
 | (1.7) |
а — коэффициент температуропроводности, м 2 /с;
q V — мощность внутренних источников тепла, Вт/м3;

Для того, чтобы решить основную задачу теории теплопроводности необходимо к дифференциальному уравнению, которое имеет бесчисленное множество решений, добавить условия однозначности. В условия однозначности входят:
геометрические условия, определяющие форму и размер тела;
физические параметры материала;
начальные условия в момент времени τ=0 ;
Граничные условия могут быть заданы тремя различными способами:
Граничные условия 1 рода.
В этом случае задается распределение температуры по всей поверхности тела 
Граничные условия 2 рода.
В этом случае задается распределение плотности теплового потока на поверхности тела и изменение этого распределения во времени

Граничные условия 3 рода.
Задается температура окружающей среды или внешнего источника тепла и закон теплообмена на границе между жидкостью и газом 
Основные понятия. Расчетные формулы



Детали, служащие для соединения отдельных элементов машин и строительных конструкций – заклепки, штифты, болты, шпонки – воспринимают нагрузки, перпендикулярные их продольной оси.
Справедливы следующие допущения.
1. В поперечном сечении возникает только один внутренний силовой фактор – поперечная сила Q.
2. Касательные напряжения, возникающие в поперечном сечении, распределены по его площади равномерно.
3. В случае если соединение осуществлено несколькими одинаковыми деталями, принимается, что все они нагружены одинаково.
Условие прочности при срезе (проверочный расчёт):
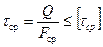
где Q – поперечная сила
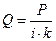
Fср 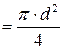
[τср] – допускаемое напряжение на срез, зависящее от материала соединительных элементов и условий работы конструкции. Принимают [τср]= (0,25…0,35)·σт, где σт – предел текучести.
Также справедливо: 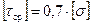
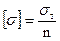
Если толщина соединяемых деталей недостаточна или материал соединяемых деталей более мягкий, чем у болта, штифта и т.д., то стенки отверстий обминаются, и соединение становится ненадежным, происходит смятие. При смятии действуют только нормальные напряжения – σ. Площадь смятия фактическая – это полуцилиндр, расчётная – это проекция полуцилиндра на диаметральную плоскость. Fсм 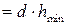
Расчетные формулы и расчеты



4.1. Приступая к вычислениям, необходимо рассчитать истинное значение температуры мокрого термометра tм ′ по формуле:

где tм − показание мокрого термометра в психрометре, °С;
Δ − ошибка в процентах от измеренной разности (tс – tм), определяемая по графику (рис. 2) в зависимости от скорости потока;
tс − температура по сухому термометру, °С.
Рис. 2. График для определения величины ошибки
к показаниям мокрого термометра при разной скорости воздуха
4.2. Атмосферное давление находится с учетом температурного расширения столбика ртути барометра по формуле:

4.3. Перепад давления воздуха в воздухомере ΔР:
где ρ – плотность воды в U-образном вакуумметре, равная 1000 кг/м 3 ;
g – ускорение свободного падения, равное 9,81 м/сек 2 ;
Н – показание вакуумметра («горло») воздухомера, переведенное в м вод.ст.
4.4. Плотность воздуха по состоянию в «горле» воздухомера ρв

где R –газовая постоянная воздуха, равная 287 Дж/кг·°К.
4.5. Расход воздуха G

4.6. Средняя скорость потока W определяется по уравнению

где F – площадь проходного сечения для потока воздуха, равная величине 0,0177, м 2 ;
4.7. Плотность воздуха ρ в рассматриваемом сечении при атмосферном давлении определяется по формуле

4.8.Определение относительной влажности:
а) по психометрической формуле

где рм − давление насыщения водяного пара при измеренной температуре мокрого термометра;
рн − давление насыщения водяного пара при температуре сухого термометра.
Величины рм и рн находятся по таблицам термодинамических свойств воды и водяного пара или по рекуррентной формуле полинома:

Поправочный коэффициент А, учитывающий влияние скорости воздуха, находится по формуле:

где В − барометрическое давление; W − скорость воздуха, м/сек.
б) по I−d диаграмме (рис.3).
4.9. Абсолютная влажность воздуха ρп определяется по уравнению:

Здесь и далее φ – относительная влажность в долях единицы;
Rп – газовая постоянная водяного пара равная 462 Дж/(кг·град);
рн − давление водяного пара при температуре сухого термометра, Па;
4.10. Влагосодержание воздуха определяется по формуле (8).
4.11. Теплосодержание (энтальпия) влажного воздуха находится по формуле (11).
4.12. Парциальное давление пара во влажном воздухе определяется по формуле:

4.13. Результаты расчетов по формулам и найденные по I-d диаграмме влажного воздуха должны быть продублированы в форме сводной таблицы.
Расчетная формула



интеграл может быть взят по любому пути соединяющему (1) и (2)
если (1) и (2) лежат на силовой линии, то в качестве линии, соединяющей (1) и (2) нужно взять силовую.
Понятие потенциала можно ввести для любого потенциального векторного поля. (потенциал гравит. силы, потенциал скорости и т.д.)
Потенциал Часто в качестве точки (2) выбирают точку, потенциал которой по определению = 0.
В теории – такая точка бесконечно удаленная: 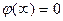
Замечание Это можно сделать лишь тогда, если заряды располагаются в ограниченной области пространства и их нет на бесконечности.
На практике 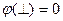
Потенциал электростатического поля в т. B(x,y,z) назыв.
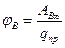
Расчетная формула:
Потенциал поля точечного заряда
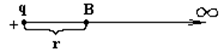 Рис. 18 Рис. 18 |
Путь из точки B в ∞ может быть любым, т.к. поле потенциально. Наиболее удобно выбрать L вдоль радиуса вектора, проведенного из точечного заряда
El = Er = E(r); => 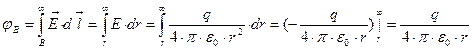
Т.к. поле точечного заряда фундаментально => для нахождения потенциала поля системы зарядов нужно применить принцип суперпозиций:
потенциал поля системы точечных зарядов равен сумме потенциалов, издаваемых в рассматриваемой точке каждым из зарядов.
а) потенциал поля системы точечных зарядов:
б) потенциал поля непрерывного распределения зарядов:
Применение формулы поля точечного заряда и принципа суперпозиций составляет основу метода непосредственного интегрирования и позволяет рассчитать потенциал поля новой системы зарядов. Графически потенциал изображается в виде эквипотенциальных поверхностей и линий на которой он принимает постоянное значение = const.
Примеры расчета потенциала
(I) Равномерно заряженная бесконечная нить. (Рис. 19)
Дано: 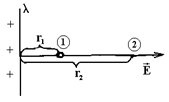
Т.к. поле нити имеет осевую симметрию и 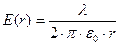
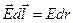
Основные расчетные формулы для решения
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ
«МОНИТОРИНГ И ЭКСПЕРТИЗА БЕЗОПАСНОСТИ ЖИЗНЕДЕЯТЕЛЬНОСТИ»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Белгородский государственный технологический университет
А.Н. Лопанов, И.А. Иванченко, Н.В.Трапезникова
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ
«МОНИТОРИНГ И ЭКСПЕРТИЗА БЕЗОПАСНОСТИ ЖИЗНЕДЕЯТЕЛЬНОСТИ»
Утверждено учёным советом университета в качестве
учебно-методического пособия для магистрантов направления
20.04.01 – Техносферная безопасность профиля «Безопасность
технологических процессов и производств» и аспирантов
направлений 20.06.01-Техносферная безопасность профиля «Охрана труда», 08.06.01- Техника и технологии строительства профиля
Доктор геолого-минералогических наук, профессор,
заведующий отделом геологии и геоинформатики
ОАО «ВИОГЕМ» В.А.Дунаев
Доктор технических наук, профессор Белгородского
государственного технологического университета
им. В. Г.Шухова Г.И. Тарасова
Учебно-методическое пособие включает методики расчетов, примеры расчетов и задания к выполнению практических работ. Оно позволит студентам качественно подготовиться к выполнению практических работ по дисциплине «Мониторинг и экспертиза безопасности жизнедеятельности».
Издание предназначено для магистрантов направления 20.04.01 – Техносферная безопасность профиля «Безопасность технологических процессов и производств» и аспирантов направлений 20.06.01-Техносферная безопасность профиля «Охрана труда», 08.06.01- Техника и технологии строительства профиля «Охрана труда».
Учебное пособие публикуется в авторской редакции.
УДК 614.8(07)+504.06(07)
ББК 68.9я7+20.1я7
(БГТУ) им. В. Г. Шухова, 2017
Оглавление
Введение
Мониторинг и экспертиза являются важнейшими элементами оценки опасностей технологических процессов и природных систем – безопасности жизнедеятельности человека в техносфере.
Мониторинг и экспертиза безопасности жизнедеятельности приобрели в настоящее время характер актуальной проблемы государственного масштаба.
Успешное изучение курса студентами возможно при наличии соответствующей учебной литературы. Одной из основных задач в подготовке квалифицированного специалиста по данному направлению является умение оценивать состояние окружающей среды с позиции безопасности жизнедеятельности.
В данном учебно-методическом пособии приведены методики и методы контроля и расчета безопасного состояния природно-технических систем, позволяющие более глубоко освоить изучаемый материал и подготовится к выполнению расчетно-графического задания по дисциплине «Мониторинг и экспертиза безопасности жизнедеятельности».
Для различных бассейнов рек
| Наименование бассейнов рек | Административный участок | Показатель δ2 |
| Нева (устье) Северная Двина (устье) Дон (устье) Северский Донец Дон Кубань Обь Енисей Амур Волга (устье Оки) | Санкт-Петербург, Псковская обл. Архангельская, Вологодская области Тамбовская обл. Белгородская, Харьковская области Ростовская обл. Краснодарский край Новосибирская обл. Красноярский край Хабаровский край Московская, Тульская, Орловская области | 0,47 0,22 1,63 3,79 1,87 2,60 0,92 0,19 0,19 2,60 |
Ущерб от сброса примесей, влияющих на содержание кислорода, оценивают по общей массе кислорода, растворенного в воде, необходимого для полного окисления веществ, а показатель относительной опасности веществ, влияющих на содержание кислорода, равен 0,33.
Приведенная масса загрязнения водоемов бактериальной микрофлорой зависит от отношения коли-индекса в сбросе и его нормативного содержания:

где 


Производственные и бытовые отходы обезвреживают различными методами переработки или складируют на свалках, отвалах. В зависимости от методов обезвреживания, складирования происходит вторичное загрязнение атмосферы, воды, почвы. Уровень вторичного загрязнения биосферы зависит от химического состава отходов, их массы, распределения по составу в различных участках экологической системы.
При отчуждении земельных ресурсов ориентировочную оценку эколого-экономического ущерба проводят по формуле:

где 



Удельный ущерб от выброса загрязнителя в почву равен 2 руб/т для неорганических отходов, 3 руб/т для отходов бытовых свалок и органических веществ.
Показатели относительной ценности земельных ресурсов приведены в табл. 1.2.
Канцерогенные риски
Линейный характер зависимости между канцерогенным риском и дозой канцерогенного вещества выражается простой формулой:
где r – индивидуальный канцерогенный риск; под ним следует понимать дополнительный риск (дополнительно к уже существующей вероятности заболеть раком) онкологического заболевания, вызываемый поступлением данного канцерогена; D – доза канцерогена, попавшего в организм человека; Fr – коэффициент пропорциональности между риском и дозой, называемый фактором риска.
Фактор риска Fr показывает, насколько быстро возрастает вероятность онкозаболевания при увеличении дозы канцерогена, поступившего в организм человека с воздухом, водой или пищей. Фактор риска еще называют коэффициентом наклона (SlopeFactor), так как он характеризует угол наклона прямой зависимости «риск – доза» (рис. (а)). Очевидно, что чем больше угол наклона, тем больше угроза здоровью.
Единица фактора риска Fr – [мг/(кг·сут)] –1 ; она обратно пропорциональна единице среднесуточного поступления канцерогена. Фактор риска количественно характеризует увеличение угрозы здоровью в результате ежедневного поступления данного канцерогена в количестве 1 мг, отнесенного к 1 кг массы тела человека.
Часто индивидуальный канцерогенный риск вычисляют по формуле:
где m – среднесуточное поступление канцерогена с воздухом, водой или с пищей, отнесенное к 1 кг массы тела человека, мг/(кг·сут).
Удобство расчета риска r по этой формуле заключается в том, что в результате перемножения величин m иFr получается безразмерная величина.
Значения факторов риска определяются, как правило, в результате опытов на животных.
В таблице ниже приведены значения факторов риска Fr (в порядке его возрастания) при поступлении в организм человека ряда канцерогенов с водой и пищей.
Значение факторов риска
| Канцерогены | Fr, [мг/(кг·сут)] –1 | Канцерогены | Fr, [мг/(кг·сут)] –1 |
| Свинец и его соединения Бензол Пентахлорфенол Хлорбензол ДДТ Кадмий и его соединения Трихлорэтилен | 8,5·10 –3 5,5·10 –2 0,12 0,27 0,3 0,38 0,4 | Тетрахлорэтилен Мышьяк Винилхлорид Бериллий, оксид Полихлорированные бифенилы Бенз(а)пирен Бериллий (сульфат) Диоксины (смесь) | 0,54 1,75 1,9 7,0 5,0 12 3·10 3 1,6·10 5 |
При решении задач, связанных с потреблением питьевой воды, среднесуточное поступление m канцерогена с водой на 1 кг массы тела человека определяется по формуле:

где С – концентрация канцерогена в питьевой воде, мг/л; v – скорость поступления воды в организм человека, л/сут (считается, что взрослый человек выпивает ежесуточно 2 литра воды); f – количество дней в году, в течение которых происходит воздействие канцерогена; Тр – количество лет, в течение которых происходит воздействие канцерогена; Р – средняя масса взрослого человека, принимаемая равной 70 кг; Т – усредненное время воздействия канцерогена, в качестве которого принимается средняя продолжительность жизни человека, считающаяся равной 70 годам (25550 сут).
После того, как вычислено среднесуточное поступление m канцерогена, приведенное к 1 кг массы тела человека, рассчитывают индивидуальный канцерогенный риск r по формуле:
В случае воздействия нескольких канцерогенов полный риск выражается суммой отдельных рисков:
Коллективный канцерогенный риск R определяется формулами:
где N – количество человек, подвергающихся данному риску.
Риск возникновения пожара
На основании статистических данных, накопленных при эксплуатации однотипных ТСЗЛ, вычисляют параметры потоков скрытых и явных отказов:
где Σnc, Σnя – суммарное число скрытых и явных отказов, выявленных приэксплуатации m однотипных ТСЗЛ (однотипными считаются ТСЗЛ одинаковой конструкции, функционального назначения и с близкимитактико-техническими параметрами);ti–наработка i –го ТСЗЛ.
Вычисляют интенсивность восстановления μ работоспособности ТС по формуле:
Среднее время до восстановления tв работоспособности ТСЗЛ определяют по статистическим данным. Формулу (1.81) применяют в случае, когда к восстановлению работоспособности ТСЗЛ приступают немедленно после обнаружения явного отказа. Если же к восстановлению работоспособности приступают после некоторого времени задержки, обусловленной административными или иными причинами, в формуле вместо tв подставляют tя, которое включает tв и время задержки по указанным причинам.
Вероятность Р(Nж) возникновения пожара с числом одновременных жертв Nж до 5 человек включительно за время t на объекте (в городе, регионе, стране) с номинальной численностью населения N вычисляют по формуле:
где λ – интенсивность потока пожаров определенного типа (табл. 1.4).
Практических работ
Номер задачи выбирается, согласно последней цифре зачетной книжки или по выбору преподавателя.
Исходные данные для расчета НДС
Задача 10. Найти НДС для веществ, обладающих лимитирующим токсикологическим действием, если расход воды в стоке 1 м 3 /с, их ПДК равны 0,01; 0,05; 0,1 мг/л, а концентрации составляют 100, 9, 3 мг/л соответственно.
Задание 11. В водоем для рыбохозяйственных целей сбрасывают сток, содержащий ацетон и фенол в концентрациях 100:1 соответственно. Рассчитать нормативный допустимый сброс (НДС) загрязняющего вещества, если средняя глубина водоема 2,3 м, а расстояние от места сброса до контрольной точки отбора проб воды на качество воды – 100 м. Расход воды 10,8 м 3 /ч, фоновая концентрация загрязняющего вещества 3,7; 0 мг/л. ПДК для ацетона и фенола принять равными 2,2; 0,001 мг/л.
Задание 12. Оценить концентрацию загрязняющего вещества в реке на расстоянии 500 м от места сброса, Расход воды в стоке 1 м 3 /с, средняя глубина реки 2 м, ширина реки 15 м, линейная скорость движения воды 0,2 м/с, концентрация загрязняющего вещества в стоке 10 г/л, фоновая концентрация вещества в реке 0,2 г/л.
Практических работ
Основные задачи расчётно-графического задания научить студентов:
— правильно оценивать опасность веществ и негативных воздействий в конкретных условиях эксплуатации технологических комплексов,
— применять методы расчета параметров для решения практических задач защиты человека, окружающей среды;
— разрабатывать мероприятия по защите окружающей среды и человека от негативного воздействия различных факторов;
— пользоваться технической, нормативной и справочной литературой.
Порядок оформления практической работы
Расчётно-графическое задание включает выполнение расчётов по темам закреплённых программой курса. Расчётно-графическое задание следует оформлять на листах формата А4 (210´297 мм); размеры полей: левое – 20 мм, правое – 10 мм, верхнее – 15 мм, нижнее – 20мм.
Текст печатается на одной стороне листа через 1,5 интервала, шрифт TimesNewRoman (кегль 14), отступ красной строки – 1,27 см., выравнивание – по ширине.
Разрешается использовать компьютерные возможности акцентирования внимания на определенных терминах, принципах, формулах, применяя шрифты разной гарнитуры.
Задания к практической работе
По математической модели
В процессе выполнения данного задания необходимо получить математическую модель процесса очистки воды от соединений ртути; найти оптимальные параметры процесса, при которых содержание ртути в сбросах минимально.
Построение математических моделей технологических процессов природных явлений основано на использовании специальных методов планирования эксперимента. Планирование эксперимента – это управление процессом, явлениями при неполном знании механизма явления процесса.
Планирование эксперимента рассматривают как одно из направлений кибернетики, основные идеи которой сформулированы в работах английского математика Рональда Фишера в 1930-1935 гг. и развиты в 1950-1957 гг. Боксом, Уилсоном и Хантером.
Методы планирования эксперимента базируются на получении математической модели в виде полинома.

где b0, bi, bij, bii – коэффициенты полинома; х – факторы, влияющие на процесс, явление (например, давление, температура и т.д.); y – переменная состояния объекта исследования.
Наиболее простой вид имеет линейный полином уравнения:
Линейный полином получают при помощи специальной установки эксперимента по определенному плану, представленному в виде матрицы планирования эксперимента.
Уровнем фактора называют значение параметра, которое фиксируется и изменяется при проведении процесса, например, х1 – температура, 60°С, 80°С; х2 – время 100 с, 140 с.
Средние значения уровней факторов называются нулевыми уровнями 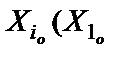

Значение фактора, прибавление которого к нулевому уровню дает верхний уровень, а вычитание – нижний уровень, называют интервалом варьирования
Область определения факторов – это их нижние и верхние уровни.
Каждую точку факторного пространства изображают в кодированной форме:

Основное преимущество факторного эксперимента заключается в одновременном варьировании всех факторов, что приводит к снижению ошибки в оценке коэффициентов полинома в N раз (N – общее число опытов).
Организация матриц планирования ПФЭ 2 2 …2 4 показана в табл.3.1.
Исходные данные и результаты крутого восхождения