Что вычисляет функция mod
Остаток от деления — функция Mod
Чтобы получить остаток от деления n на m, нужно воспользоваться функцией Mod[n,m]. Наименьший возможный остаток в этом случае равен нулю, а наибольший. Как вы думаете, чему равен наибольший возможный остаток? «Конечно, m-1», — возможно, подумали вы. Ну, что же, я, конечно, приветствую ваши глубокие познания в теории чисел, ибо именно так написано во всех классических учебниках по этой дисциплине, если, конечно, именно в этом месте нет какой-либо досадной опечатки. Но должен вас разочаровать: вы не угадали. Зато, надеюсь, вам будет приятно узнать, что возможности функции Mod значительно шире, чем требуется для решения задач из задачников по классической теории чисел. Дело в том, что аргументы этой функции могут быть не только целыми (это предусмотрено классическими учебниками теории чисел), но и вещественными и даже комплексными! А во множестве вещественных чисел, как вы, надеюсь, еще помните, полно сюрпризов. Но сначала давайте рассмотрим простейший случай целых аргументов.
Ну вот, при делении 7 на 5 остаток равен 2. Просто и понятно, даже в уме можно вычислить. Вот еще один пример.
Тоже в уме, и тоже просто и понятно. Но вот несколько примеров с вещественными числами. 
Теперь, надеюсь, вы поняли, что множество значений Mod[n,m] не имеет набольшего элемента. Можно лишь утверждать, что при вещественных m и n 0
Документация
Остаток после деления (операция с модулем)
Синтаксис
Описание
Примеры
Остаток после деления от скаляра
Вычислите 23 по модулю 5.
Остаток после деления от вектора
Остаток после деления для положительных и отрицательных величин
Найдите остаток после деления для набора целых чисел и включая положительные и включая отрицательные величины. Обратите внимание на то, что ненулевые результаты всегда положительны, если делитель положителен.
Остаток после деления для отрицательного делителя
Найдите остаток после деления отрицательным делителем для набора целых чисел и включая положительные и включая отрицательные величины. Обратите внимание на то, что ненулевые результаты всегда отрицательны, если делитель отрицателен.
Остаток после деления для значений с плавающей точкой
Входные параметры
a — Дивиденд
скаляр | вектор | матрица | многомерный массив
Если a duration массив и m числовой массив, затем значения в m обработаны как числа 24-часовых дней.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | duration | char
m — Делитель
скаляр | вектор | матрица | многомерный массив
Если m duration массив и a числовой массив, затем значения в a обработаны как числа 24-часовых дней.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | duration | char
Больше о
Различия Между mod и rem
Концепция остатка после деления исключительно не задана, и две функции mod и rem каждый вычисляет различное изменение. mod функция приводит к результату, который является или нулем или имеет тот же знак как делитель. rem функция приводит к результату, который является или нулем или имеет тот же знак как дивиденд.
Оба варианта имеют свое использование. Например, в обработке сигналов, mod функция полезна в контексте периодических сигналов, потому что его выход является периодическим (с периодом, равным делителю).
Отношения конгруэтности
Ссылки
[1] Knuth, Дональд Э. Искусство Программирования. Издание 1. Аддисон Уэсли, 1997 pp.39–40.
Расширенные возможности
«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
Арифметика выполняется с помощью выходного класса. Результаты не могут совпадать с MATLAB ® из-за различий в погрешностях округления.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
64-битные целые числа не поддерживаются.
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Смотрите также
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация MATLAB
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
Оператор Mod
Возвращает остаток от деления двух чисел.
Синтаксис
результат = number1 Mod number2
Синтаксис оператора Mod состоит из следующих частей:
| Part | Описание |
|---|---|
| result | Обязательный элемент; любая числовая переменная. |
| число1 | Обязательный элемент; любое цифровоезначение. |
| число2 | Обязательный элемент; любое цифровое значение. |
Примечания
Оператор модуля (остатка) делит число1 на число2 (числа с плавающей запятой при этом округляются до целого) и возвращает остаток в аргументе результат. Например, в следующем выражении A (результат) равно 5.
Обычно типом данных атрибута результат является Byte, вариант Byte, Integer, вариант Integer, Long или Variant, содержащий значение Long, независимо от того, является ли результат целым числом. Дробные части отсекаются.
Однако если любое из выражений имеет значение Null, объект результат будет иметь значение Null. Любое выражение со значением Empty обрабатывается как 0.
Пример
В этом примере оператор Mod возвращает только остаток от деления двух чисел. Любые числа с плавающей запятой предварительно округляются до целого.
См. также
Поддержка и обратная связь
Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
Оператор mod — остаток от деления. Что такое mod?
Оператор mod обозначается символом % и является оператором деления по модулю. Он возвращает остаток от деления 1-го операнда на 2-й и широко используется в разных языках программирования для решения ряда задач.
Оператор mod в Java
В Java operator mod может работать как с целыми числами (byte/int/short/long), так и с плавающей точкой (byte/int/short/long). Давайте приведём пример работы оператора mod при делении:
После выполнения этой программы вы получите результат следующего вида:
Как видим, оператор mod — это прекрасный способ найти остаток от деления. Зачем это может понадобиться на практике? Например, при нахождении кратности числа и определении, является ли некоторое число, введённое с клавиатуры, чётным. Также с помощью оператора mod можно узнать, делится ли одно число на другое без остатка или определить последнюю цифру числа. В общем, оператор mod очень полезен при решении различных задач по программированию.
Оператор mod в SQL
Не менее интересно использование mod в базах данных. Аналогично, mod находит остаток от деления. При этом вместо mod можно задействовать операцию %, делающую то же самое. Синтаксис в SQL следующий:
Но можно написать и иначе, используя % :
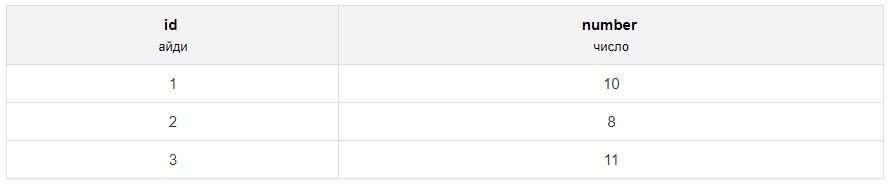
Давайте приведём пример использования mod в базах данных. Вот, например, таблица numbers:
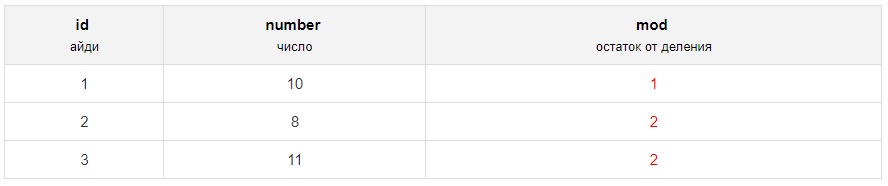
Найдём остаток от деления столбца number на три:
В результате запрос SQL выберет следующие строки:
Но, как мы уже говорили выше, этот же запрос можно без проблем переписать:
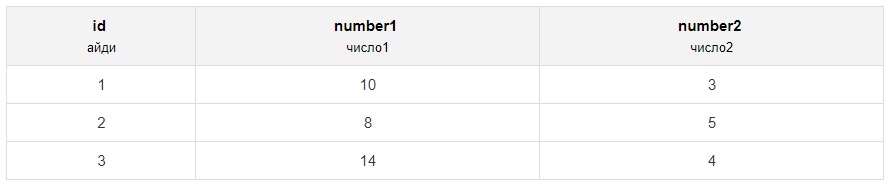
Идём дальше. Теперь возьмём таблицу посложнее:
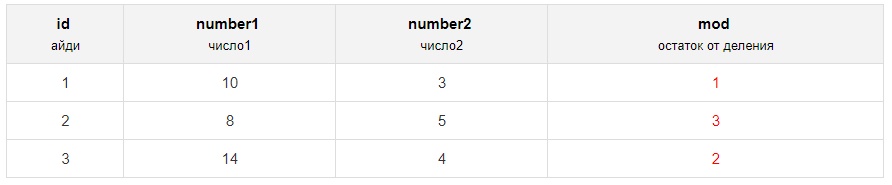
Здесь найдём остаток от деления столбца number1 на number2:
Получим следующие строки:
Опять же, этот же самый запрос можно оформить иначе:
А где вы используете mod? Пишите в комментариях!